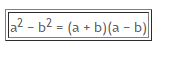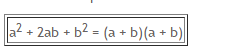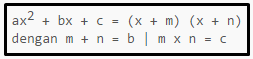Rumus Pemfaktoran Aljabar – Rumus pemfaktoran aljabar yaitu sebuah rumus untuk menyatakan sebuah bentuk persamaan aljabar menjadi sebuah bentuk perkalian aljabar atau faktorisasinya . Dalam pembahasan sebelumnya , kita telah mengenal istilah faktorisasi aljabar . Faktor dari sebuah bilangan yaitu bilangan pembagi habis suatu bilangan tersebut . Contohnya bentuk aljabar ab = a x b , faktorisasinya = a dan b . bentuk aljabar a(x + y ) maka faktorisasinya a dan (x+y ) . Untuk memahami lebih dalam mengenai rumus pemfaktoran , perhatikan penjelasan dibawah ini .
Metode Pemfaktoran Aljabar
- Sifat Distributif
Sifat distributif dapat digunakan untuk memfaktorkan bentuk aljabar dengan mencari FPB dari bentuk alhabar tersebut . Persamaan yang dapat diselesaikan menggunakan sifat distributif yaitu bentuk aljabar :
Contoh soal :
Faktorkan bentuk – bentuk aljabar berikut ini :
a. 3x2 y + 6xy2
b. 15pq + pq2 r
c. 2a2 + 4a2 y
d. 2a2 + 8a2 b
e. 3x2 y + 9xy2
Penyelesaian :
Untuk menyelesaikan soal di atas maka langkah pertama yaitu mencari Fpb dari bentuk aljabar tersebut .
a. 3x2 y + 6xy2
FPB dari 3x2 y + 6xy2 adalah 3xy
jadi bentuk pemfaktorannya : 3x2 y + 6xy2 = 3xy ( x + 2y )
b. 15pq + pq2 r
FPB dari 15pq + pq2 r adalah pq
jadi bentuk pemfaktorannya : 15pq + pq2 r = pq ( 15 + qr )
c. 2a2 + 4a2 y
FPB dari 2a2 + 4a2 y = 2a
jadi , bentuk pemfaktorannya : 2a2 + 4a2 y = 2a ( a + 2ay )
d. 2a2 + 8a2 b
FPB dari 2a2 + 8a2 b = 2a
jadi , bentuk pemfaktorannya : 2a2 + 8a2 b = 2a ( a + 4ab )
e. 3x2 y + 9xy2
FPB dari 3x2 y + 9xy2 = 3xy
jadi , bentuk pemfaktorannya : 3xy ( x + 3y )
2. Pemfaktoran Dalam Bentuk selisih kuadrat
Cotoh soal :
Faktorkan bentuk aljabar berikut ini :
a. x2 – 2 2
b. 42 − x2
c. 5 2 − x2
d. 4x2 − 16
e. 9x8 − 4y4
Penyelesaian :
a. x2 – 2 2 = ( x+ 2 ) ( x – 2 )
b. 42 − x2 = ( 4 + x ) ( 4 – x )
c. 5 2 − x2 = ( 5 + x ) ( 5 – x )
d. 4x2 − 16
= (2x)2 – ( 4 ) 2
= ( 2x + 4 ) ( 2x – 4 )
e. 9x8 − 4y4
= (3x4 )2 – ( 2y2 )2
= ( 3x4 + 2y2 ) ( 3x4 – 2y2 )
3. Pemfaktoran Aljabar Dalam Bentuk Kuadrat yang sempurna
atau
Contoh Soal :
a. a2 + 10a + 25
b. x2 − 16 x + 64
c. 16b2 − 20bc + 25c2
d. p2 – 10p + 25
e. 16a2 + 16a + 4
Penyelesaian :
a. a2 + 10a + 25 = ( a + 5 ) ( a + 5 )
b. x2 − 16 x + 64 = ( x – 8 ) ( x – 8 )
c. 16b2 − 40bc + 25c2
= ( 4b -5c ) ( 4b – 5c )
d. p2 – 10p + 25 = ( p – 5 ) ( p – 5 )
e. 16a2 + 16a + 4
= ( 4a + 2 ) ( 4a + 2 )
4. Pemfaktoran Aljabar Dalam Bentuk ax2 + bx + c = 0 , dan a = 0
Contoh soal :
a. a 2 + 7a + 12
b. p2 + 6p +8
c. n2 + 9n + 14
d. q2 + 9q + 18
Penyelesaian :
Langkah pertama , yaitu menentukan dua angka yang apabila di jumlah sama dengan angka tengah dan apabila di kali sama dengan huruf yang ke tiga .
a. a 2 + 7a + 12 = ( a + 4 ) ( a + 3 )
karena angka 4 dan 3 diatas apabila 4 + 3 = 7 dan 4 x 3 = 12
b. p2 + 6p + 8 = ( p + 2 ) ( p + 4 )
karena angka 2 dan 4 diatas apabila 2 + 4 = 6 dan apabila 2 x 4 = 8
c. n2 + 9n + 14 = ( n + 2 ) ( n + 7 )
karena angka 3 dan 7 diatas apabila 2 + 7 = 9 , dan 2 x 7 = 14
d. q2 + 9q + 18 = ( q + 3 ) ( q + 6 )
karena angka 3 dan 6 diatas apabila 3 + 6 = 9 dan 3 x 6 = 18
5. Pemfaktoran Aljabar Dalam Bentuk ax2 + bx + c = 0 , dan a ≠ 0
ax2 + bx + c = 0
Contoh soal
a. 5x2 + 13 – 6 = 0
Pembahasan :
5x2 + 13 – 6 = 0
a x c = m x n , m + n = b
jadi , angka yang cocok adalah 15 dan -2 , karena 5 x -6 = 15 x – 2 dan 15 + (-2 ) = 13 maka
5x2 + 13 – 6
< = > 5x2 + 15x -2 x -6
< = > 5x ( x + 3 ) – 2 ( x + 3 )
< = >( 5x – 2 ) ( x + 3 )
b. 2x2 + 11x – 6
Pembahasan :
2x2 + 11x – 6
a x c = m x n , m + n = b
jadi , angka yang cocok adalah 12 dan – 1 , karena 2 x -6 = 12 x -1 dan 12 + ( -1 ) = 11 maka
2x2 + 11x – 6
<=> 2x2 + 12x – x – 6
<=> 2x ( x + 6 ) -( x + 6 )
<=> ( 2x -1 ) ( x + 6 )
Demikian penjelasan mengenai Cara untuk menghitung Rumus Pemfaktoran Bentuk aljabar secara lengkap . Dan telah dijelaskan beserta dengan contohnya . Inti dari pemfaktoran bentuk aljabar yaitu harus memahami FPB dari suatu bilangan . Karena jika tidak mengetahui maka akan sulit untuk mempelajarinya . Selain itu juga untuk memudahkan dalam menyelesaikan soal pemfaktoran aljabar langkah pertama harus memahami bentuk dari persamaan tersebut . Bentuk dari persamaan aljabar telah dijelaskan di atas . Selalu semangat untuk belajar , karena ilmu matematika adalah ilmu yang sangat mudah untuk dipelajari apabila yang mempelajari itu bersungguh – sungguh .