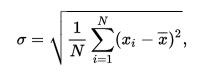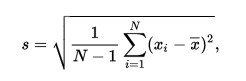Rumus Simpangan Baku – Pengertian Simpangan Baku atau Deviasi Standar ialah suatu bentuk ukuran sebaran Statistik yang paling lazim singkatnya dan Simpangan Baku juga dapat mengukur bagaimana Nilai – Nilai Data tersebar karena Simpangan Baku didefinisikan sebagai Akar Kuadrat Varians dan juga bisa didefinisikan sebagai rata – rata jarak penyimpangan titik – titik data yang diukur dari nilai rata – rata data tersebut.
Lalu Simpangan Baku merupakan bilangan tak negatif yang memiliki satuan yang sama dengan datanya, sebagai contoh jika suatu data diukur dalam satuan Meter maka Simpangan Baku juga dapat diukur dlm satuan Meter pula. Perlu kalian ketahui para pelajar dan pembaca bahwa Istilah Simpangan Baku untuk pertama kali diperkenalkan oleh seorang yang bernama Karl Pearson ditahun 1894 didlm bukunya yg berjudul On The Dissection Of Asymmetrical Frequency Curves, beliau (Karl Pearson) merupakan pendiri Institute Of Statistika University College London.
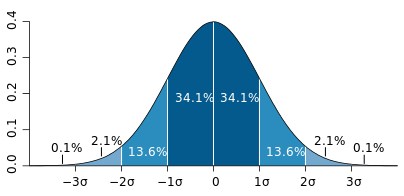
Menurut Karl Pearson dalam Statistik mengatakan bahwa wilayah data yg berada diantara +/- 1 Simpangan Baku akan berkisar 68.2 persen, wilayah data yg berada diantara +/- 2 Simpangan baku akan bernilai berkisar 95.4 persen dan Wilayah Data yg berada diantara +/- 3 Simpangan Baku akan memiliki nilai berkisar 99.7 persen. Mungkin bisa kalian lihat secara lebih detail tentang Rumus Simpangan Baku dalam Ilmu Statistika dibawah ini, yang terbagi menjadi Dua Rumus yakni Rumus Simpangan Baku Populasi dan Simpangan Baku Sampel.
Rumus Simpangan Baku Populasi Statistika
Didalam Rumus Simpangan Baku Untuk Populasi disimbolkan dengan σ atau Sigma dan didefinisikan dengan rumus yang telah ditulis dibawah ini.
Rumus Simpangan Baku Sampel Statistika
Sedangkan untuk Simpangan Baku Sampel disimbolkan dengan s dan di definisikan dengan rumus seperti dibawah ini.
Dimana {x1, x2, . . .xn} merupakan nilai data dari Sampel dan 
Contoh Soal Simpangan Baku Statistika
1. Seorang Pelajar telah mengikuti ulangan Matematika sebanyak 10 kali dan dia mendapatkan nilai dari kesepuluh ulangan tersebut antara lain nilai 91, 79, 80, 86, 75, 90, 88, 93, 100 dan 87. Berapakah Simpangan Baku dari Nilai Ulangan Matematika seorang Pelajar tersebut ?
Jawaban
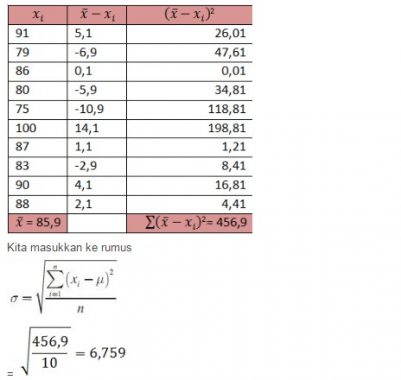
Soal diatas dapat diselesaikan dengan memakai Rumus Simpangan Baku Populasi sehingga kita cari dulu nilai rata – ratanya.
Nilai Rata – Rata = (91 + 79 + 80 + 86 + 75 + 90 + 88 + 93 + 100 + 87) / 10 = 859 / 10 = 85.9
Jika dalam Soal Simpangan Baku menyebutkan Sample bukan Populasi maka menggunakan Rumus Simpangan Baku Sample (n-1), misalnya dari 500 penduduk diambil 150 Sample untuk diukur berat badannya.
Mungkin seperti itu saja pembahasan yang bisa kami sampaikan tentang Rumus Simpangan Baku Statistika dan semoga kalian sebagai pembaca sudah bisa mengenal lebih dalam lagi tentang Simpangan Baku karena Simpangan Baku Statistik ini sering muncul di tingkat Sekolah Menengah Atas (SMA) sehingga kalian sebagai pelajar atau Siswa Siswi tingkat SMA harus bisa mengenal tentang salah satu pelajaran Statistika Simpangan Baku karena tidak mungkin Rumus ini dapat keluar di Ujian Sekolah maupun Ujian Nasional.