Materi, Jenis2, Dan Contoh Pertidaksamaan Rasional – Halo pengguna artikel rumusrumus.com sudahkah kamu siap untuk melanjutkan pembahasan mengenai materi, jenis2, dan contoh pertidaksamaan rasional ? beserta dengan bagaimana cara menyelesaikannya ? Jangan khawatir semua yang kamu butuhkan ada disini. Agar kamu tidak bingung, marilah simak pembahasan materi pertidaksamaan rasional secara rinci dibawah ini.

Definisi Pertidaksamaan Rasional
Perhatikanlah masing – masing bentuk pertidaksamaan berikut.
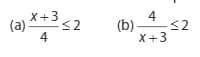
Kedua bentuk pertidaksamaan diatas ialah memuat suatu bentuk pecahan atau yang dikenal dengan “rasional”. Tetapi, apakah bentuk keduanya termasuk dalam kategori pertidaksamaan rasional ?. Tidak, hanya bentuk (b) lah yang merupakan pertidaksamaan rasional karena memuat variabel pada penyebutnya tersebut. Sedangkan (a) bukanlah bentuk pertidaksamaan rasional karena penyebutnya tidak memuat dalam variabel tersebut.
Dapat disimpulkan bahwa, pertidaksamaan rasional merupakan pertidaksamaan yang berbentuk pecahan atau rasional dimana penyebutnya memuat suatu variabel.
Jenis – Jenis Pertidaksamaan Rasional
Tahukah anda bahwa pertidaksamaan rasional ini dapat dibedakan menjadi dua bentuk, yaitu pertidaksamaan rasional linear dengan pertidaksamaan rasional kuadrat. Bentuk umum dari kedua pertidaksamaan ini ialah sebagai berikut :
1. Pertidaksamaan Rasional Linear

2. Pertidaksamaan Rasional Kuadrat

Sifat – Sifat Pertidaksamaan Rasional
Ingatkah kamu mengenai suatu sifat – sifat dalam pembagian pada bilangan bulat tersebut ? Supaya kamu dapat ingat kembali, perhatikan sifat – sifatnya berikut penjelasannya :
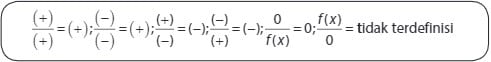
Berdasarkan dari sifat – sifat pembagian yang sudah dijabarkan diatas, dapat diperoleh sifat – sifat pertidaksamaan rasional seperti berikut ini :

Terdefinisi adalah g(x) ≠ 0, dengan demikian ini dapat diperoleh sifat berikut dibawah ini :


Dengan hal demikian dapat diperoleh sifat berikut ini :

Langkah – Langkah Penyelesaiannya
Setelah mengetahui pengertian, jenis – jenis, serta sifat – sifat yang sudah dijelaskan diatas tersebut, berikut ini merupakan suatu langkah – langkah didalam penyelesaian pertidaksamaan rasional atau pertidaksamaan pecahan ini, maka simaklah agar dapat menyelesaikan soal dengan mudah menggunakan teknik ini :
A. Langkah pertama pindahkan seluruh suku ke dalam satu ruas misalnya kita ambil ruas kiri sehingga tidak tersisa suku artinya tersisa nol di dalam ruas kanan. Begitu perlu untuk diperhatikan anda, jika kita begitu dilarang untuk mengkali (x) silang penyebut maupun pembilang antarruas tersebut. Mengapa begitu dilarang ? Karena nilai yang belum diketahui begitu mungkin dapat mengubah bentuk pertidaksamaan tersebut jika kita melakukan kali silang tersebut.
B. Langkah kedua, lakukanlah operasi aljabar. Sudah pernah belajar kan mengenai operasi jabar ini ? Ya, tujuannya biasanya agar memperoleh atau mendapatkan bentuk yang lebih sederhana, sesudahnya kamu lakukan pemfaktoran yang mana dapat difaktorkan agar memperoleh ataupun mendapatkan nilai x tersebut.
C. Langkah terakhir adalah menyusun nilai x tersebut ke dalam garis bilangan yang ada. Bagaimana halnya dengan pertidaksamaan pangkat tinggi maupun besar, tentukan dahulu tanda yang terdapat pada masing-masing daerah dengan melakukannya secara manual. Caranya yaitu dengan mengambil satu nilai x di dalam daerah tersebut kemudian sesudahnya menguji hasil tersebut pada bentuk peridaksamaan yang ada.
Contoh Soal Beserta Cara Jawabannya
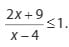
1. Tentukan cara penyelesaian pada pertidaksamaan disamping ini –>
Berikut Cara Penyelesaiannya :
Langkah awal nyatakan suatu pertidaksamaan diatas dalam bentuk umumnya seperti ini :
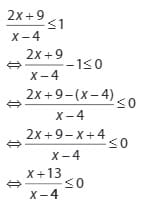
Karena hasil langkah awal pertidaksamaan tersebut bernilai negatif atau sama dengan nol, maka berlaku sebagai berikut :
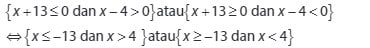
Setelah menentukan irisan pada daerah tersebut, diperoleh bentuk seperti dibawah ini :
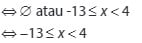
Dapat disimpulkan dari hasil penyelesaian yang didapat dari pertidaksamaan pada soal pertama adalah −13 ≤ x < 4.
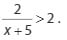
2. Tentukan cara penyelesaian pada pertidaksamaan disamping ini –>
Berikut Cara Penyelesaiannya :
Langkah awal nyatakan suatu pertidaksamaan diatas dalam bentuk umumnya seperti berikut ini
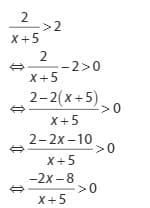
Karena hasil langkah awal pertidaksamaan tersebut sudah bernilai positif atau tidak nol hasilnya, maka berlaku sebagai berikut :
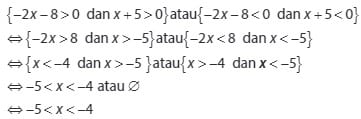
Dapat disimpulkan dari hasil penyelesaian yang didapat dari pertidaksamaan pada soal kedua ini adalah −5 < x < −4.
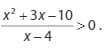
3. Tentukan cara penyelesaian pada pertidaksamaan disamping ini –>
Berikut Cara Penyelesaiannya :
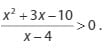
Karena sudah diketahui bahwa pertidaksamaan contoh ke 3 bernilai positif atau tidak nol hasilnya, maka berlaku sebagai berikut :
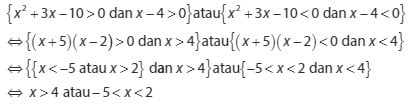
Dapat disimpulkan dari hasil penyelesaian yang didapat dari pertidaksamaan pada soal ketiga ini adalah −5< x < 2 atau x > 4
Pertidaksamaan rasional adalah suatu pertidaksamaan dimana berbentuk pecahan maupun rasional yang penyebutnya memuat suatu variabel tertentu.
Istilah lain dari pertidaksamaan rasional ini adalah “pertidaksamaan pecahan”.
1. Pertidaksamaan rasional linear
2. Pertidaksamaan rasional kuadrat
Demikianlah pembahasan artikel kali ini, semoga bermanfaat dan menjadi ilmu pengetahuan baru bagi para pembaca.
Baca juga artikel lainnya :