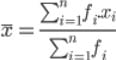Rumusrumus.com kali ini akan membahas tentang distribusi frekuensi, macam-macam distribusi, rumus distribusi, langkah-langkah menyusun tabel distribusi, cara hitung rata-rata atau mean, serta penjelasan aturn pembulatan. untuk lebih jelasnya, simak penjelasan dbawah ini
Pengertian Disribusi Frekuensi
Distribusi frekuensi ialah daftar nilai data (berupa nilai individual ataupun nilai data yang telah di kelompokkan dalam selang interval tertentu) dan yang disertai nilai frekuensi yang sesuai.
Pengelompokkan data dalam beberapa kelas dimaksudkan guna ciri-ciri penting data itu bisa terlihat. Daftar frekuensi tersebut mampu memberikan gambaran yang khas tentang keragaman data. Sifat keragaman data sangat penting untuk diketahui, karena dalam pengujian-pengujian statistik selanjutnya harus selalu memperhatikan sifat dari keragaman data. Tanpa memperhatikan sifat keragaman data, penarikan suatu kesimpulan umumnya tidak sah.
Variasi yang amat penting dari distribusi frekuensi dasar ialah dengan memakai nilai frekuensi relatifnya, yang disusun dalam bentuk persentase frekuensi tiap kelas dari total semua frekuensi / banyaknya data.
Distribusi Frekuensi Relatif
Distribusi frekuensi relatif merupakan suatu jumlah persentase yang menyatakan jumlah banyaknya data pada suatu kelompok.
Terlebih dahulu menghitung persentase pada tiap kelompok. Distribusi akan memberikan informasi yang lebih jelas tentang posisi masing-masing bagian pada keseluruhan, Guna melihat perbandingan antara kelompok yang satu dengan kelompok yang lainnya.
Distribusi frekuensi relative menyatakan proporsi data yang ada pada suatu kelas interval. Distribusi frekuensi relatif mencakup batas kelas yang sama seperti TDF, Akan tetapi frekuensi yang dipakai bukan frekuensi aktual melainkan frekuensi relatif.

Langkah Menyusun Tabel Distribusi Frekuensi
- Urutkan data, Umumnya diurutkan dari nilai yang terkecil, Tujuannya agar range data bisa diketahui dan mempermudah penghitungan frekuensi tiap kelas
- Tentukan range (rentang atau jangkauan) Range = nilai maksimum – nilai minimum
- Tentukan jumlah kelas. Jangan terlalu banyak ataupun terlalu sedikit, berkisar antara 5 dan 20, tergantung dari banyak dan sebaran datanya.
Aturan Sturges: Banyak kelas = 1 + 3.3 log n (n adalah banyaknya data) - Tentukan panjang/lebar kelas
interval (p) Panjang kelas (p) = [rentang]/[banyak kelas] - Tentukan nilai ujung bawah kelas interval pertama
Saat menyusun TDF, pastikan kelas tidak tumpang tindih sehingga nilai-nilai pengamatan masuk tepat ke dalam satu kelas. Pastikan juga tidak ada data pengamatan yang tertinggal
Contoh:
menyusun tabel distribusi frekuensi nilai ujian mahasiswa (Tabel 1).
1. Berikut nilai ujian mahasiswa yang telah diurutkan:
35 38 43 48 49 51 56 59 60 60 61 63 63 63 65 66 67 67 68 70 70 70 70 71 71 71 72 72 72 73 73 74 74 74 74 75 75 76 76 77 78 79 79 80 80 80 80 81 81 81 82 82 83 83 83 84 85 86 86 87 88 88 88 88 89 90 90 90 91 91 91 92 92 93 93 93 95 97 98 99
2. Range
[nilai tertinggi – nilai terendah] = 99 – 35 = 64
3. Banyak Kelas
Tentukan banyaknya kelas .
Lihat nilai Range = 64, banyak kelas sekitar 6 atau 7. Sebagai latihan, pakai aturan Sturges.
banyaknya kelas = 1 + 3.3 x log(n)
= 1 + 3.3 x log(80)
= 7.28 ≈ 7
4. Panjang Kelas
Panjang Kelas = [range]/[banyak kelas]
= 64/7
= 9.14 ≈ 10
5. Tentukanlah nilai batas bawah kelas pada kelas pertama. Nilai ujian paling kecil = 35
Penentuan nilai batas bawah kelas bebas, selama nilai terkecil masih masuk ke dalam kelas tersebut.
Mean atau Rata-rata Hitung
Mean atau Rata-rata Hitung adalah suatu nilai hasil dari membagi jumlah nilai data dengan banyaknya jumlah data.
Mean berupa nilai yang menunjukkan pusat dari nilai data tersebut dan merupakan nilai yang mampu mewakili dari keterpusatan data dan umumnya disebut juga sebagai nilai rata-rata dari data yang ada.
Mean merupakan satu ukuran guna memberikan gambaran yang lebih jelas dan singkat tentang sekumpulan data
Rumus Mean
Jika berbentuk tunggal, maka rumus mean adalah
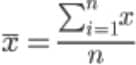
Aturan Pembulatan
Jika dihadapkan dengan bilangan pecahan yang mempunyai angka desimal dengan banyak jumlah angka di belakang koma.
Dalam Statistika ada aturan pembulatan bilangan yang dijadikan acuan dalam mengolah data satistika. ada tiga aturan pembulatan, yaitu :
Aturan 1
Andai angka terkiri dari angka yang dihilangkan kurang dari 5, maka angka terkanan dari angka yang mendahuluinya tidak berubah atau tetap
Contoh : 50,16482 ton dibulatkan hingga dua angka di belakang koma jadi 50,16 ton angka yang harus dihilangkan yaitu 482 dengan angka terkiri 4 (kurang dari 5). maka angka terkanan dari angka yang mendahuluinya (yaitu 6) tetap (tidak berubah)
Aturan 2
Jika angka terkiri dari angka yang harus dihilangkan lebih dari 5 atau angka 5 diikuti oleh angka bukan nol semua, jadi angka terkanan dari angka yang mendahuluinya bertambah dengan satu.
Contoh : 50,14652 dibulatkan sampai dua angka di belakang koma menjadi 50,15 50,14501 akan dibulatkan hingga dua angka di belakang koma menjadi 50,15
Aturan 3
Andai angka terkiri dari angka harus dihilangkan sama dengan 5 atau angka 5 diikuti oleh angka nol semua, jadi angka terkanan dari angka yang mendahuluinya tetap jika angka tsb genap, dan bertambah satu jika angka tsb ganjil.
Contoh : 50,14500 dibulatkan sampai dua angka di belakang koma menjadi 50,14 50,13500 akan dibulatkan hingga dua angka di belakang koma menjadi 50,14
Macam-Macam Distribusi Frekuensi
Jika ditinjau dari jenisnya yaitu
- Distribusi frekuensi numerik
- Distribusi kategorikal
Ditinjau dari nyata tidaknya frekuensi yaitu
- Distribusi frekuensi absolut
- Distribusi frekuensi relatif
Ditinjau dari kesatuannya yaitu
- Distribusi frekuensi satuan
- Distribusi frekuensi kumulatif
Distribusi frekuensi numerik
Distribusi frekuensi numerik yaitu Distribusi frekuensi yang didasari pada data-data kontinum, yaitu data yang berdiri sendiri dan berupa suatu deret hitung
Distribusi frekuensi kategorikal
Distribusi frekuensi kategorikal yaitu Distribusi frekuensi yang didasari oleh data yang terkelompok. Jika data masih berbentuk kontinum, maka harus diubah dahulu menjadi data kategorikal dan selanjutnya beru dicari frekuens masing-masing kelompok.
Hal yang harus diperhatikan ketika menentukan kelas bagi distribusi frekuensi kategorikal yaitu:
- Jumlah kelas
- Lembar kelas
- Batas kelas
Distribusi frekuensi absolut
Distribusi frekuensi absolut yaitu suatu jumlah bilangan yang menyatakan jumlah banyaknya data pada suatu kelompok tertentu. Disusun berdasarkan data apa adanya, sehingga tidak menyulitkan para peneliti dalam membuat distribusi ini.
Distribusi frekuensi relative
Distribusi frekuensi relatif yaitu suatu jumlah persentase yang menyatakan jumlah banyaknya data pada suatu kelompok tertentu.
Dalam hal ini pembuat distribusi terlebih dahulu harus mampu menghitung persentase pada setiap kelompok. Distribusi akan memberikan informasi yang lebih jelas tentang posisi masing-masing bagian dalam keseluruhan
Demikianlah penjelasan mengenai artikel ini, Semoga bermanfaat
Artikel Terkait :