Invers Matriks – Matriks adalah salah satu bahan pembelajaran untuk matematika yang terdiri dari susunan numerik dalam kurung. Sementara itu, menurut pendapat para ahli, matriks didefinisikan sebagai satu set angka yang disusun dalam baris atau kolom dalam tanda kurung kotak atau tanda kurung biasa.
Bahan matriks dibagi menjadi beberapa jenis sebagai matriks penentu dari matriks terbalik, matriks yang berdekatan, dan sebagainya. Namun, di antara semua jenis materi dalam matriks, ada satu bahan yang banyak diminati, yaitu rumus matriks terbalik dan contoh soal matriks terbalik.
Bahkan, kita dapat menemukan materi yang berisi rumus matriks atau perkalian matriks dalam matematika di sekolah menengah. Faktanya, masih banyak siswa yang kesulitan mempelajari rumus matriks.
Penggunaan kata terbalik dalam matriks terbalik yang sama sering ditemukan dalam aljabar, yang berarti bahwa itu adalah kebalikannya.
Karena itu kebalikan dari 3 adalah 1/3, jadi kebalikan dari bilangan rasional a adalah 1 / a. Ini tentu juga berlaku untuk matriks.
Namun, dalam matriks, ada rumus terpisah untuk menghitung invers. Rumus terbalik dapat dibagi menjadi dua jenis, yaitu rumus untuk pesanan 2×2 dan rumus untuk pesanan 3×3.
Dalam artikel kali ini saya akan menjelaskan matriks invers dari urutan 2×2 dan urutan 3×3 bersama – sama dengan contoh – contoh soal invers.
Berikut ini ulasan lebih lanjut.
Rumus Invers Matriks Beserta Contoh Soal
Kami menemukan berbagai contoh masalah seperti perkalian matriks invers 3×3 atau matriks invers 2×2 pada matriks invers 4×4.
Faktanya, metode dan metode penyelesaian masalah dengan matriks tidak jauh berbeda sampai Anda memahami rumus matriks terbalik itu sendiri. Jadi bagaimana kita dapat dengan cepat mempelajari rumus matriks?
Kebalikan dari matriks ditunjukkan dengan nama tertentu sebagai huruf besar dan karenanya meningkat menjadi -1.
Misalnya, sebagai matriks B, kebalikan dari matriks B & supmin; ¹ ditulis. Sebelum kita membahas rumus matriks terbalik 2×2 dan mengatur 3×3 bersama dengan contoh masalah matriks terbalik.
Saya akan membagikan beberapa karakteristik inversi. Sifat-sifat dari matriks terbalik adalah sebagai berikut :
- AA‾¹ = A‾¹A = I
- AB‾¹ = B‾¹A‾¹
- (A‾¹)‾¹ = A
- Jika XA = B, maka X = BA-¹
- Jika AX = b, maka X = A-¹B
Secara umum, rumus invers matriks dapat ditulis sebagai berikut :
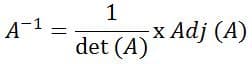
Keterangan :
- A‾¹ = Invers Matriks (A)
- det (A) = Determinan Matriks (A)
- Adj (A) = Adjoin Matriks (A)
1. Invers Matriks 2×2
Setelah menjelaskan rumus matriks terbalik dan sifat-sifatnya di atas. Selanjutnya, saya akan menjelaskan cara menemukan inversi matriks 2×2.
Tentu saja, Anda akan menemukan 2×2 terbalik dengan rumus di atas dan saat Anda membuatnya lebih mudah daripada matriks pesanan 3×3.
Untuk perhitungan terbalik ini 2×2 sesuai dengan metode cepat. Namun, metode cepat ini hanya berlaku jika pesanannya 2×2.
Sebelum itu, pertama-tama kita harus menemukan nilai dari matriks tetangga. Rincian lebih lanjut dapat ditemukan dalam contoh berikut.
[su_box title=”Contoh Soal Matriks 2×2″ box_color=”#0031e8″]
Menentukan matriks invers dari!
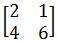
Jawaban :
Untuk menghitung kebalikan dari matriks, metode cepat digunakan. Sebelum menggunakan rumus matriks terbalik di atas. Pertama-tama kita harus menemukan nilai adjoin dahulu.
Untuk menemukan matriks invers 2×2 yang berdekatan, kita hanya perlu menukar atau memindahkan elemen yang posisinya ada di baris pertama kolom pertama dengan elemen-elemen di baris kedua kolom kedua.
Berikutnya, baris kedua dari kolom pertama dan baris pertama dari kolom kedua dikalikan dengan -1. Hasilnya adalah sebagai berikut.
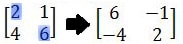
Selanjutnya, cari determinan matriks
det = (2 × 6) – (4 × 1)
= 12 – 4
= 8
Setelah nilai adjoin dan determinan matriks diketahui. Kemudian masukkan rumus matriks di atas. Hasilnya adalah :
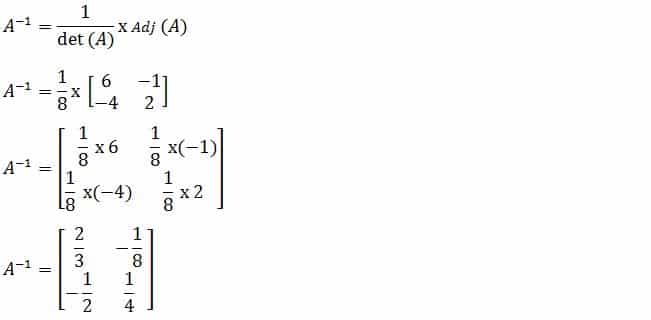
[/su_box]
2. Invers Matriks 3×3
Rumus kebalikan dari matriks 3×3 sesuai dengan urutan 2×2 sebagai berikut :
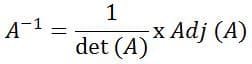
Hampir seperti dalam pencarian perkalian dari matriks 2×2 di atas, pertama-tama kita harus menemukan determinan untuk menemukan matriks invers 3×3. Penentu urutan 3×3 dapat dicari dengan dua metode:
- Metode Sarrus
- Metode Minor – Kofaktor
Secara umum, determinan terbalik dari matriks 3×3 lebih mudah untuk dihitung menggunakan metode Sarrus. Metodenya adalah sebagai berikut :
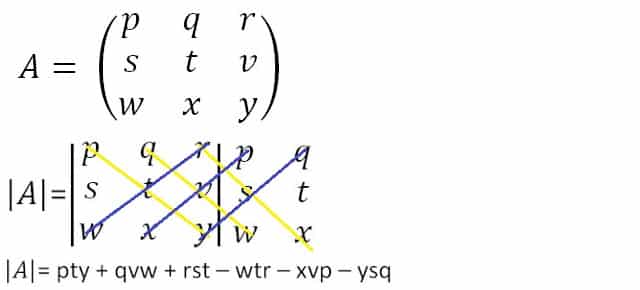
Selanjutnya kita mencari matriks tetangga dalam rumus matriks terbalik. Untuk menghitung matriks yang berdekatan, pertama-tama kita perlu menentukan nilai matriks kofaktor.
Matriks kofaktor adalah matriks yang elemennya dimodifikasi oleh nilai-nilai determinan yang nilainya bukan kolom dan tidak selaras dengan elemen sumber.
Kemudian, sebagai alternatif, tanda positif atau negatif diberikan sebagai berikut :
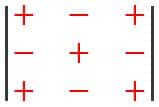
Jadi, Anda lebih memahami rumus invers dari matriks 3×3. Saya akan memberikan contoh masalah yang berkaitan dengan rumus terbalik ini. Berikut adalah contoh masalah matriks terbalik.
[su_box title=”Contoh Soal Matriks 3×3″ box_color=”#0031e8″]
Matriks A dikenal sebagai berikut :

Menentukan kebalikan dari matriks di atas A!
Jawaban :

[/su_box]
Ini adalah penjelasan dari rumus matriks terbalik dan contoh masalah matriks terbalik yang bisa saya jelaskan dalam artikel ini.
Bahkan, mengerjakan berbagai masalah matriks sangat mudah. Kita membutuhkan lebih banyak latihan langsung dan menghafal setiap rumus perkalian matriks.
Hal lain yang perlu kita ingat adalah menemukan perkalian dari matriks invers.
Kita harus menemukan determinan dan matriks yang berdekatan. Ini adalah rumus matriks invers absolut.
Baca Juga :