Poligon

Poligon – Hallo gaes, jumpa lagi dengan saya. Sekarang saya akan mengulas tentang apa itu poligon, jenis, ciri – ciri, serta gambarnya. Untuk itu, yuukk langsung simak saja penjelasan dibawah ini.

Pengertian Poligon

Poligon terdiri dari dua kata, poly dan gone. Arti kata Poly bermacam-macam. Sedangkan makna gone adalah titik. Oleh karena itu, bentuk ini dapat diartikan sebagai banyak sudut.

Ada dua jenis poligon tertutup dan terbuka. Dia dikatakan tertutup ketika titik awal dan titik akhir bertemu pada suatu titik. Bentuk terbuka ditandai dengan titik awal dan akhir yang tidak bertemu pada suatu titik.

Oleh karena itu, representasi data dari kelompok modul poligon terkandung dalam poligon terbuka.

Jenis Poligon

1. Beraturan

Bentuk beraturan yang keduanya merupakan bingkai yang sudutnya sama dan memiliki sisi yang sama, yaitu mereka memiliki semua sisi dengan panjang yang sama dan semua sudut bagian dalam sama.

2. Tidak Beraturan

Bentuk tidak beraturan yang sudutnya tidak sama besar.

3. Convex

Semua sudut kurang dari 180 derajat

4. Concave

Salah satu sudutnya adalah 180 derajat

Ciri Ciri Poligon

Nama tersebut disesuaikan berdasarkan jumlah sisi, salah satunya terkait dengan jumlah awalan Yunani yang diakhirnya ditambah dengan gon.

1. Segi empat tepat
2. Segi empat sama
3. Segi empat selari
4. Rombus
5. Trapesium
6. Lelayang

Langkah Untuk Menampilkan Data Dalam Bentuk Poligon

Penyajian data kelompok dari modul poligon dimulai dengan perubahan data acak dalam tabel data kelompok.

Ini digunakan untuk mempermudah teman idschool memetakan nilai data dengan cara yang lebih teratur dan terstruktur.

Selanjutnya, teman-teman idschool harus menentukan titik tengah setiap kelas. Langkah terakhir adalah mengatur titik tengah setiap kelas ke nilai frekuensi yang sesuai.

1. Menampilkan data acak dalam tabel data grup.
2. Menentukan nilai pusat dari setiap kelas.
3. Buat bidang di mana data ditampilkan dalam bentuk poligonal dan sudah berisi pusat dari masing-masing kelas untuk salah satu sumbunya.
4. Memetakan data berdasarkan nilai frekuensi untuk setiap kelas.
5. Menghubungkan pusat setiap kelas sesuai dengan nilai frekuensi untuk membentuk garis lurus yang menghubungkan titik-titik.
6. Proses penyajian data kelompok bentuk poligon telah selesai.

Contoh Penyajian Dalam Bentuk Poligon

Berikut ini adalah data evaluasi matematika dari kelas empat puluh siswa. Daftar nilai matematika yang diperoleh oleh 40 siswa ditunjukkan dalam data acak berikut.

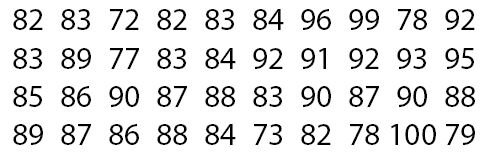
Presentasi acak dari data di atas dalam tabel data grup dapat dianggap sebagai berikut.

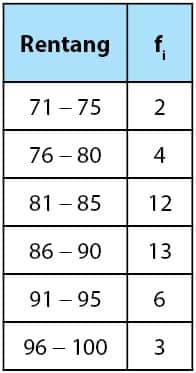
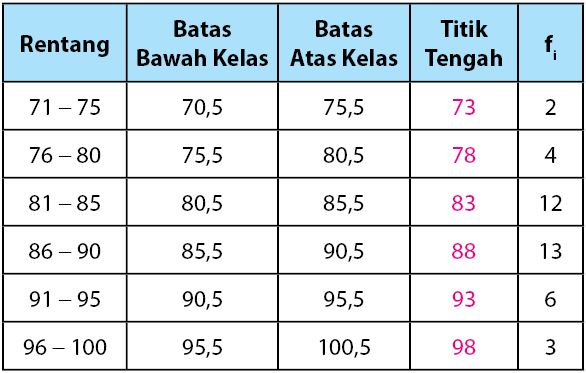
Langkah selanjutnya dalam menyajikan data kelompok modul poligonal adalah menentukan nilai rata-rata setiap kelas. Nilai rata-rata diperoleh dengan menjumlahkan batas bawah kelas dan batas atas kelas dan kemudian membagi hasilnya dengan dua.

Sebagai contoh, satu kelas memiliki interval antara 71 – 75. Dengan demikian, batas atas dan bawah dari kelas masing-masing adalah 70,5 dan 75,5. Lalu, titik tengah kelas adalah 73.

Hasil lengkapnya tercantum dalam tabel berikut.

Selanjutnya, bidang Cartesius disiapkan yang berisi nilai pada sumbu x dan data frekuensi pada sumbu y. Selain batas interval kelas untuk setiap kelas. Kurang lebih, bidang gambar bidang diperoleh sebagai berikut.

Kemudian tautkan data terkait antara data nilai titik tengah setiap kelas dan frekuensi yang lebih rendah. Seperti terlihat pada gambar di bawah ini.

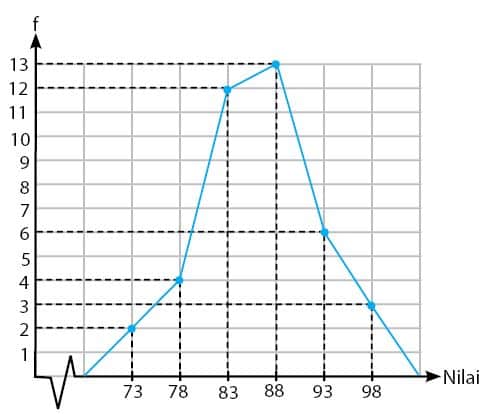
Itulah penjelasan cara untuk menyajikan data kelompok dalam bentuk poligon. Cara di mana data disajikan dijelaskan dalam bentuk data acak dan kemudian dalam bentuk tabel data kelompok.

Akhirnya, sesuai dengan tujuan yang diberikan di bagian judul, yang merupakan representasi dari data kelompok modul poligon.

Baca Juga :

• Cara Membuat Histrogram
• Invers Matriks
• Memahami Macam – Macam Pola Bilangan Dalam Matematika