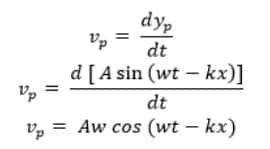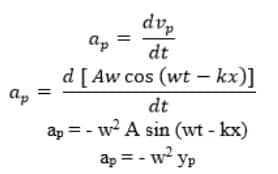Rumusrumus.com kali ini akan membahas tentang materi fisika yaitu gelombang berjalan yang meliputi rumus rumus dari percepatan, kecepatan sudut dan bilangan gelombang serta kecepatan sudut dan contoh soalnya
Pengertian Gelombang Berjalan
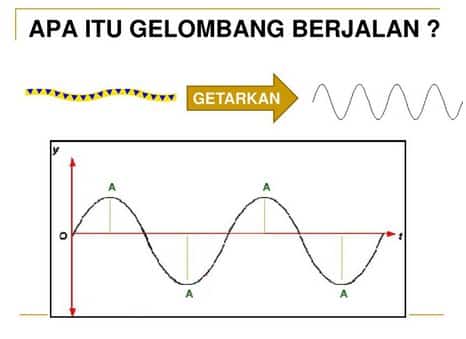
Gelombang berjalan adalah jenis gelombang yang mempunyai sifat amplitudo yang sama pada setiap titik yang dilalui.
Rumus persamaan Gelombang Berjalan :
y = A sin (ωt – kx)
Persamaan ini didapatkan dari persamaan umum gelombang
yaitu y = A sin ωt dan ω = 2π/ T
Sehingga y = A sin (2π t/T)
Dari persamaan y = A sin (2π t/T), yang dimaksud t ialah waktu.
Karena gelombang berjalan mengalami perubahan jarak, kecepatan dan waktu sehinnga bisa diambil kesimpulan persamaan gelombang y = A sin (2 π (t2-t1)/T)
kemudian t2 = x/v
sehingga
y = A sin 2πt/T – 2πx/T.v karena v = λ.f , v = λ/T maka λ = T.v
y = A sin 2πt/T – 2π.x/ λ k = konstanta gelombang = 2π/ λ
y = A sin 2πt/T – kx
y = A sin (ωt – kx)
Rumus Kecepatan Sudut
Kecepatan sudut disimbolkan dengan ω bersatuan rad/s.
ω = 2πf = 2π/T
f adalah frekuensi
T adalah periode gelombang.
Rumus Bilangan Gelombang
Bilangan gelombang disimbolkan dengan k bersatuan rad/m.
k = 2π/λ
λ adalah panjang gelombang.
Rumus Cepat Rambat Gelombang
Cepat rambat gelombang dirumuskan
v = λ x f atau v = ω/k
Kecepatan dan Percepatan Gelombang Berjalan
Kecepatan Getar Partikel Gelombang Berjalan
Pada gelombang berjalan, sudah diketahui bentuk persamaan umum simpangannya yaitu yp = A sin (wt – kx) dengan arah getar pertama ke atas dan arah rambat ke kanan (sumbu x positif). Dari persamaan tersebut, Maka bisa diperoleh persamaan kecepatan getar partikel sebagai berikut :
Kecepatan getar partikel bernilai maksimum jika nilai cos (wt – kx) = 1
Sehingga : vp maks = Aw
Percepatan Getar partikel pada Gelombang berjalan
Jika telah mengetahui kecepatan getar partikel, maka bisa diketahui juga percepatan getar partikel sebagai berikut :
Percepatan getar partikel akan bergerak maksimum jika nilai sin (wt – kx) = -1
sehingga : ap = w2 A
Sudut Fase
Pada persamaan gelombang berjalan yang sudah didapatkan, yaitu :
y = A sin (ωt – kx)
y = A sin 2π ( t/T – x/λ)
Terdapat besar sudut dalam fungsi sinus 2π ( t/T – x/λ) yang disebut juga dengan sudut fase gelombang (0)
sehingga : 0B = (wt – kx) = 2π ( t/T – x/λ)
Fase
Penjelasan mengenai suatu tahap yang sudah dicapai oleh suatu gerak yang terus menerus atau berkala seperti gelombang dengan membandingkan dengan gerak gelombang lain yang sejenis dengan frekuensi yang sama disebut fase. Hubungan sudut fase (0) dengan fase yp adalah maka : yp = (t/T – x/λ)
Beda Fase
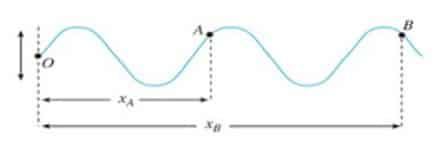
Pada titik A yang berjarak xA dari titik asal getaran O dan titik lain
B yang berjarak xB dari titik asal getaran O
Maka beda fase antara titik A dan B adalah
Dengan xb > xa
Contoh Soal
Sebuah gelombang transversal merambat yang menurut persamaan y = 0,5 sin (8πt – 2πx) m.
Tentukanlah arah gelombang dan Amplitudo gelombangnya
Jawab :
arah gelombang ( sumbu x +) karena persamaan bertanda negatif maka gelombang bergerak ke arah kanan sedangkan amplitudo gelombangnya adalah A = 0,5 m
Demikianlah penjelasan Rumusrumus.com tentang gelombang berjalan, Semoga bermanfaat
Artikel Lainya :