Rumus Perpangkatan Aljabar Matematika

Rumus Perpangkatan Aljabar – Rumus perpangkatan aljabar sama prinsipnya dengan perpangkatan pada bilangan bulat . Perpangkatan yaitu perkalian yang diulang dengan suatu  bilangan yang sama .

Rumus perpangkatan secara umum : 

Rumus Perpangkatan Aljabar :

( a + b )ⁿ  = ( a + b )  x ( a + b ) x  ( a + b ) , . . . x ( a + b )

Dengan ( a + b ) sebanyak n

Sebelum Mengetahui bagaimana cara untuk menyelesaikan perpangkatan bentuk aljabar , maka yang perlu diperhatikan yaitu :

• abⁿ   berbeda dengan (ab )ⁿ 

Dalam bentuk abⁿ  maka yang dipangkatkan n  hanya b nya saja , namun pada bentuk (ab )ⁿ   maka yang dipangkatkan n semuanya , yaitu (ab)

Contoh :

( 2a )²    = ( 2a )( 2a ) = 4a²

Sedangkan

2a²     = 2 x a x a = 2a²

• ( -ab )ⁿ  berbeda dengan  – (ab )ⁿ

Dalam bentuk ( -ab )ⁿ  ,maka yang dipangkatkan n adalah   ( -ab ) . Sedangkan dalam bentuk – (ab )ⁿ  yang dipangkatkan n adalah ab

Cara menyelesaikan Perpangkatan Aljabar 

Apabila suatu bilangan aljabar berpangkat 2 maka masih mudah dalam mengerjakannya namun bagaimana cara untuk mengerjakan atau menyelesaikan perpangkatan aljabar yag pangkatnya lebih dari 2 ?

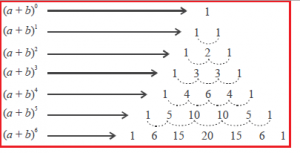
Sebelum mengetahui bagaimana cara untuk menyelesaikan perpangkatan aljabar yang lebih dari dua , kita harus mengetahui terlebih dahulu mengenai segitiga pascal . Mengapa demikian ? Karena dalam penyelesaian perpangkatan aljabar segitiga pascal sangat membantunya .

Perhatikan segitiga pascal berikut ini :

Cara penggunaan segitiga pascal dalam penyelesaian perpangkatan aljabar:

( a + b )⁰  = 1

( a + b )¹  = a + b

( a + b )²  = a²  +  2ab  + b²

( a + b )³  = a³  +  3a²b +  3ab²  + b³

( a + b )⁴  = a⁴  +  4a³b +  6a²b²  + 4ab³ + b⁴

( a + b )⁵ =  a⁵  +  5a⁴b +  10a³ b²  + 10a²b³ + 5ab⁴ + b⁵

Contoh Soal 

A . Tentukan hasil perpangkatan bilangan tersebut !

1. (-2a )² 
2. – ( 3b )³
3. ( 2xy )²

Penyelesaian

1. (-2a )²    =  (-2a)  x  (-2a )

                         = 4a²

2. – ( 3b )³    =   – { (3b) ( 3b ) ( 3b ) }

                      = – 27b³

B. Berapakah hasil perpangkatan bentuk aljabar berikut ?

1. ( -2x )² 
2. ( x + 2y)² 
3. ( x + 2 )³
4. ( 3x +  6 ) ³
5. ( -3a + 2b)²
6. (7x -8 ) ³
7. ( 3a – 2 )⁴ 
8. ( 2x – 2)²

Penyelesaian :

1. ( -2x )² = ( -2x ) x ( -2x )

                        = 4x²

2. Rumus ( a + b )² = a²  +  2ab  + b² 

maka :

( x + 2y)²   =  x²  +  2(2xy)  + 2xy²

                   =  x²  +  4xy  + 2xy²

3. Rumus ( a + b )³ = a³  +  3a²b +  3ab² + b³

maka :

( x + 2 )³  =  x³  +  3x²2 +  3×2²  + 2³

                      = x³ + 6x² + 12x + 8

4. Rumus ( a + b )³ = a³  +  3a²b +  3ab² + b³

maka :

( 3x + 6 ) ³ =  3x³  +  3(3x)²6 +  3(3x)6²  + 6³

                   =  3x³  + ( 3 . 3x . 3x . 6 )+ 3(3x)36 + 216

                  = 3x³  + (3 . 9x²  . 6 ) + 324x + 216

                 =  3x³  + 162 + 324x + 216

5. Rumus : ( a + b )² = a²  +  2ab  + b² 

Maka :

( -3a + 2b)²  = -3a²  +  2(-3a)2b  + 2b² 

                      =  -3a² + (-12ab ) + (2b . 2b )

                     =  -3a²  -12ab  + 4b² 

6. Rumus : ( a + b )³ = a³  +  3a²b +  3ab² + b³

Maka :

(7x -8 ) ³ = a³  +  3a²b +  3ab²  + b³

                = 7x³  + 3(7x)²(-8) + ( -8 )³

               = 7x³  + 1176x² – 512

Tips dalam menyelesaikan perpangkatan aljabar :

a. Memahami bentuk perpangkatan .

b. Memahami pola dalam segitiga pascal , ( a+b )ⁿ

c. Mensubstitusikan  dari bentuk perpangkatan aljabar kedalam pola  segitiga pascal .

Demikian penjelasan mengenai rumus perpangkatan bentuk aljabar . Kunci dari rumus perpangkatan bentuk aljabar yaitu memahami pola segitiga pascal dan memahami tanda – tanda bilangan . Jangan sampai salah dalam memangkatkan . Semoga bermanfaat