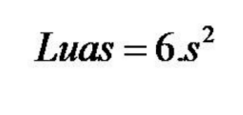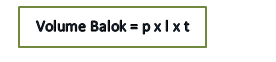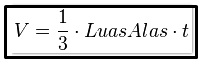Rumus Bangun Ruang Sisi Tegak |Apakah perbedaan dari rumus bangun ruang sisi lengkung dengan bangun ruang sisi tegak ? kali ini kita akan mempelajari bersama . Sebelum mempelajari itu semua , pertama kali harus mengetahui pengertian bangun ruang .
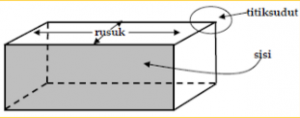
Bangun ruang merupakan suatu istilah untuk bangun matematika tiga dimensi yang memiliki panjang lebar dan tinggi atau bangun yang terdiri dari tiga unsur yaitu sisi , rusuk , titik sudut , diagonal sisi dan diagonal ruang .
- Sisi yaitu bagian suatu bangun yang membatasi bagian dalam dan luar .
- Rusuk yaitu perpotongan dua bidang sisi suatu bangun.
- Titik sudut yaitu Perpotongan tiga sisi atau rusuk .
Untuk lebih jelasnya perhatikan gambar di bawah ini :
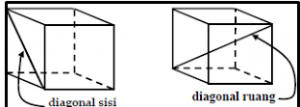
- Diagonal sisi , yaitu suatu garis yang melintang yang menghubungkan dua buah titik sudut yang letaknya tidak berurutan dalam sisi sebuah bangun dan letaknya berhadapan .
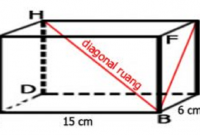
- Diagonal Ruang , yaitu sebuah garis pada bangun ruang yang menghubungkan dua buah titik sudut yang berhadapan serta tidak berurutan .
Untuk lebih jelasnya perhatikan gambar di bawah ini :
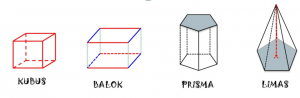
Bangun Ruang terbagi menjadi dua macam , yaitu :
- Bangun Ruang sisi Tegak , yaitu terdiri dari kubus , balok , prisma dan limas
- Bangun Ruang sisi Lengkung , yaitu terdiri dari tabung , kerucut dan bola
Pada kesempatan kali ini , yang akan kita pelajari adalah rumus bangun ruang sisi tegak .
Rumus Bangun Ruang Sisi Tegak
- Kubus
Kubus yaitu bangun ruang yang memiliki sisi yang sama dan rusuk sama panjang .
Kubus terdiri dari 6 buah bidang sisi / bidang , 8 buah titik sudut dan 12 rusuk .
Perhatikan gambar di bawah ini :
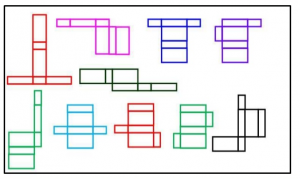
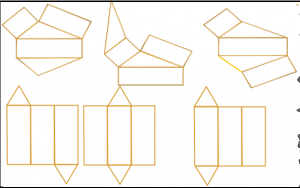
Jaring – jaring kubus:
- Luas Permukaan Kubus
Dalam sebuah kubus terdiri dari 6 bidang yang berbentuk segi empat . Sedangkan luas persegi = sisi x sisi ( s2 ), jadi luas permukaan kubus adalah 6 kali luas persegi .
- Volume Kubus
Kubus merupakan bangun ruang yang memiliki panjang rusuk sama panjang , maka dalam kubus tidak ada istilah panjang ( p ) , lebar ( l ) dan tinggi ( t ) . Namun itu semua diganti dengan sisi ( s )
Jadi , volume kubus adalah :
Volume = Luas alas x tinggi
= s x s x s
= s3
Jadi , Rumus Volume Kubus adalah :
2. Balok
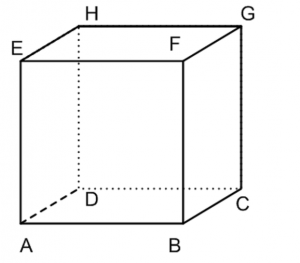
Balok merupakan bangun ruang atau bangun tiga di mensi yang bentuknya hampir sama dengan kubus , yang membedakan hanyalah ukuran rusuknya , pada kubus sama panjang sedangkan pada balok berbeda panjangnya .
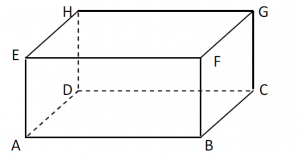
Perhatikan Gambar di bawah ini :
Setelah kita lihat gambar di atas , maka dapat kita fahami ada sisi yang kongruen . Sisi – sisi tersebut adalah :
- Sisi ABEF ,kongruen dengan sisi CDGH ( sisi depan dan belakang )
- Sisi BCFG , kongruen dengan sisi ADEH ( sisi samping kiri dan kanan )
- Sisi ABCD , Kongruen dengan sisi EFGH ( sisi atas dan bawah )
Kongruen yaitu sama dan sebangun baik panjang ataupun sudutnya .
Jaring – jaring balok
Balok terdiri atas 6 bidang sisi , 12 rusuk dan 8 titik sudut .
- Luas Permukaan Balok
Balok terdiri dari 3 sisi yang saling berhadapan ,yaitu
- Sisi ABEF ,kongruen dengan sisi CDGH ( sisi depan dan belakang )
- Sisi BCFG , kongruen dengan sisi ADEH ( sisi samping kiri dan kanan )
- Sisi ABCD , Kongruen dengan sisi EFGH ( sisi atas dan bawah )
Rumus untuk mencari luas permukaan balok adalah :
Luas ABCD = P x L
Luas ABEF = Px t
Luas BCFG = L x T
Luas Balok = 2( p x l ) + 2( p x t ) + 2( l x t )
= 2 (p x l + p x t + l x t )
Jadi , Rumus Luas permukaan Balok adalah
- Volume Balok
Volume balok = La x t
= p x l x t
Jadi , rumus volume balok adalah
3. Prisma
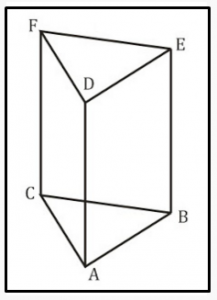
Prisma yaitu bangun ruang atau bangun tiga dimensi yang memiliki dua buah bangun yang kongruen dan saling berhadapan , dua bangun yang berhadapan tersebut disebut sebagai alas dan tutup , sedangkan yang menghubungkan ke dua bangun tersebut disebut dengan tinggi . Atau dapat di lihat dari ciri – ciri lain , bahwa prisma adalah bangun ruang yang terdiri dari sisi yang berbeda yang saling berpotongan pada titik – titik sudut . Untuk lebih jelasnya perhatikan gambar di bawah ini :
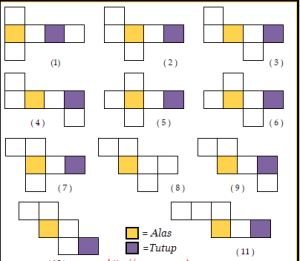
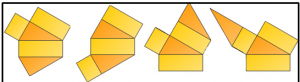
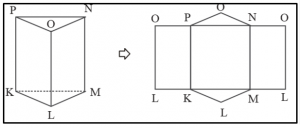
Berikut adalah beberapa contoh Jaring – jaring prisma :
- Luas Permukaan Prisma
Luas permukaan prisma , yaitu jumlah luas alas , luas tutup dan luas sisi tegak .
Perhatikan gambar prisma di bawah ini :
Luas permukaan prisma = ( Luas KLM + Luas NOP ) + ( Luas KLOP + Luas KMNP + Luas LMNO )
= ( 2 x Luas KLM ) + { ( LK x t ) + ( KM x t ) + ( LM x t ) }
= ( 2 x Luas alas ) + t ( LK + KM + LM )
= ( 2 x Luas alas ) + t x Keliling alas
Jadi , Rumus Luas permukaan prisma adalah :
Luas Permukaan Prisma = ( 2 x Luas Alas ) + t x Keliling alas
- Volume Prisma
Untuk menghitung volume prisma , yaitu harus memperhatikan alasnya . Karena rumus volume prisma tergantung dengan bentuk alasnya.
Volume prisma segi tiga =( 1/2 x alas x tinggi segitiga ) x tinggi prisma
Volume prisma segi empat = ( s x s ) x tinggi prisma
dan lain sebagainya . Dan dapat disimpulkan bahwa ruus volume prisma adalah :
Volume prisma = Luas Alas x Tinggi
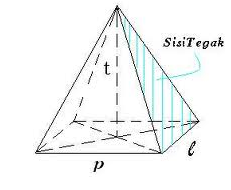
4. Limas
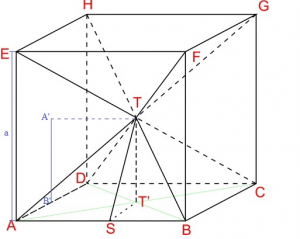
Limas merupakan bangun 3 dimensi yang memiliki sisi miring berbentuk segi tiga dan memiliki titik puncak . Tahukah anda , bahwa kubus adalah gabungan dari 6 buah limas ? perhatikan gambar di bawah ini :
Dari gambar di atas , ada 6 buah limas dengan titik puncak T dan membentuk sbuah kubus .
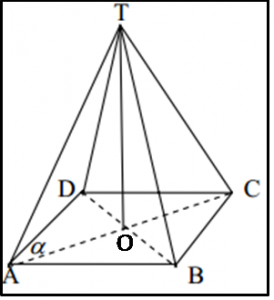
Untuk lebih jelasnya mengenai bentuk limas , perhatikan gambar di bawah ini :
- Luas Permukaan Limas
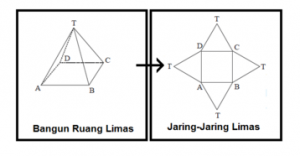
Untuk dapat menyelesaikan atau cara untuk mencari luas permukaan limas , pertama kali kita harus memahami jaring – jaring dari limas tersebut . Karena hal itu akan membantu untuk mengetahui rumus luas permukaan limas . Perhatikan gambar di bawah ini :
Dari gambar di atas , diketahui bahwa alas bangun limas tersebut berbentuk persegi empat . Jadi , rumus untuk mencari luas permukaan limas adalah :
Lpermukaan limas = L uas ABCD +( Luas ∆TAB + Luas ∆TBC + Luas TCD + Luas ∆TAD)
= Luas alas + Jumlah Luas Sisi tegak
Jadi , Rumus permukaan limas adalah :
Luas Permukaan = Luas alas + Jumlah luas Sisi Tegak
- Volume Limas
Untuk dapat memahami bagaimana rumus volume limas , maka terlebih dahulu perhatikan gambar di bawah ini :
Luas alas = p x l ( karena alasnya berbentuk persegi panjang )
Luas alas = s x s ( apabila alasnya berbentuk persegi empat )
Demikian penjelasan mengenai rumus bangun ruang sisi tegak , pada dasarnya untuk dapat memudahkan dalam memahami dan hafal mengenai rumus bangun ruang sisi tegak yaitu dengan memahami bentuk – bentuknya apakah bangun ruang sisi tegak ataukah bangun ruang sisi lengkung dan sering – seringlah untuk latihan mengerjakan dan dengan sendirinya akan hafal .