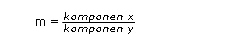Persamaan garis lurus adalah salah satu cabang ilmu matematika yang dipelajari sejak kita duduk di bangku SMP. Sebenarnya apakah yang dimaksud dengan pgl ? dan bagaimanakah rumus – rumusnya serta cara menentukannya? Simak dibawah ini.
Persamaan ini dapat diartikan juga dengan persamaan linier yaitu ada yang teriri dari satu variabel dan ada juga yang terdiri dari dua variabel. Untuk lebih jelasnya, perhatikan penjelasan – pejelasan di bawah ini.
Rumus Persamaan Garis Lurus
Sebelum kita mempelajari tentang rumus – rumusnya, kita harus memahami terlebih dahulu pengertian dan definisinya terlebih dahulu. Dan dalam sebuah persamaan garis lurus.
Ada satu komponen yang tidak dapat terlepas darinya yaitu Gradien . Apakah yang dimaksud dengan gradien? Perhaikan penjelasan di bawah ini :
A. Pengertian Persamaan Garis Lurus
Persamaan Garis lurus yaitu suatu perbandingan antara koordinat y dan koordinat x dari dua titik yang terletak pada sebuah garis.
Sedangkan garis lurus sendiri ialah kumpulan dari titik – titik yang sejajar. Dan garis lurus dapat dinyatakan dalam berbagai bentuk.
Dibawah ini beberapa contoh untuk menyatakan persamaan garis lurus, yaitu :
- y = mx
- y = -mx
- y = a
- x = a
- ax + by = ab
- ax – by = -ab
- dan lain-lain
Perhatikan gambar dibawah ini beberapa contoh grafik dan bentuk garis lurus serta cara menyatakan atau menentukannya :
[su_box title=”Contoh Cara Menentukan Persamaan Garis Lurus” box_color=”#0031e8″]
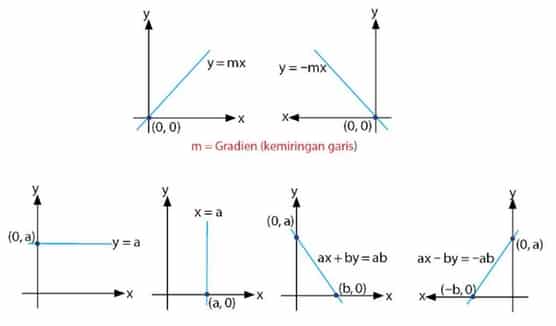
[/su_box]
B. Pengertian Gradien
Gradien yaitu Perbandingan komponen y dan komponen x , atau disebut juga dengan kecondongan sebuah garis. Lambang dari suatu gradien yaitu huruf “m”.
Gradien juga dapat dinyatakan sebagai nilai dari kemiringan suatu garis dan dapat dinyatakan dengan perbandingan Δy/Δx
Perhatikan gambar dibawah ini untuk menentukan gradien pada sebuah persamaan garis berikut :
[su_box title=”Cara Menentukan Gradien” box_color=”#0031e8″]
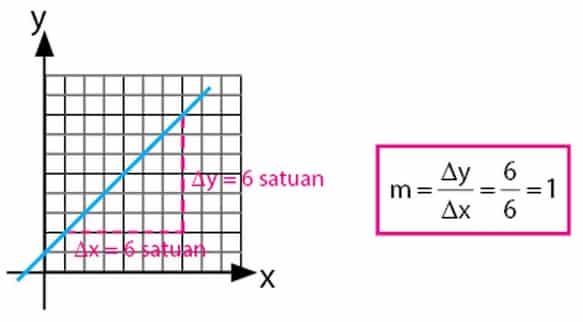
[/su_box]
Berikut ini rumus mencari gradien garis dengan beberapa jenis persamaan :
- Gradien dari persamaan ax + by + c = 0
- Gradien yang melalui titik pusat ( 0 , 0 ) dan titik ( a , b )m = b/a
m = b/a
- Gradien Yang melalui titik ( x1 , y 1 ) dan ( x2 , y2 )
m = y1 – y2 / x1 – x2 atau m = y2 – y1 / x2 – x1
- Gradien garis yang saling sejajar ( / / )
m = sama atau jika dilambangkan adalah m1 = m2
- Gradien garis yang saling tegak lurus ( lawan dan kebalikan )
m = -1 atau m1 x m2 = -1
C. Rumus Cara Menentukan
1. Persamaan Garis Lurus bentuk umum ( y = mx )
Persamaan yang melalui titik pusat ( 0 , 0 ) dan bergradien m .
Contoh :
Tentukan persamaan garis lurus yang melalui titik pusat ( 0 , 0 ) dan bergradien 2 !
Jawab : y = mx
y = 2 x
2. y = mx + c
->Persamaan garis yang / / dengan y = mx dan bergradien m
-> Persamaan garis yang melalui titik ( 0 , c ) dan bergradien m. ( 0 , c ) adalah titik potong sumbu y .
3. Persamaan Garis Lurus Yang Melalui titik ( x1 , y1 ) dan bergradien m
persamaannya yaitu :
y – y1 = m ( x – x1 )
4. Persamaan Garis Lurus Yang Melaui Dua titik yaitu ( x1 , y 1 ) dan ( x2 , y2 ) .
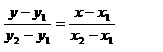
Contoh Soal
[su_box title=”Contoh Soal 1″ box_color=”#0031e8″]
Tentukan Gradien garis yang melalui titik ( 0 , 0 ) dengan titik A ( -20 , 25 ) ?
Penyelesaian :
Diketahui :
Titik ( 0 , 0 )
Titik A ( -20 , 25 )
Ditanya : m = . . .?
Jawab :
m = b / a = 25 / -20 = – 5/4
[/su_box]
[su_box title=”Contoh Soal 2″ box_color=”#0031e8″]
Tentukan Gradien garis yang melalui titik A ( -4 , 7 ) dan B ( 2 , -2 ) ?
Penyelesaian :
Diketahui :
Titik A ( -4 , 7 )
TitikB ( 2 , -2 )
Ditanya : m = . . ?
Jawab :
m= y1 – y2 / x1 – x2
m = 7 – ( -2) / -4 -2
m = 9 / -6
m = – 3/2
[/su_box]
[su_box title=”Contoh Soal 3″ box_color=”#0031e8″]
Tentukan Gradien garis dengan persamaan garis 4x + 5y – 6 = 0 ?
Penyelesaian :
Diketahui :
Persamaan 4x + 5y – 6 = 0
Ditanya : m = . . .?
Jawab :
m = -a / b
m = -4 / 5
[/su_box]
[su_box title=”Contoh Soal 4″ box_color=”#0031e8″]
Tentukan persamaan garis lurus yang melalui pusat koordinat dan bergradien – 4/5 ?
Penyelesaian :
Diketahui :
Titik pusat koordinat ( 0 , 0 )
m = -4/5
Ditanya : Persamaan garis lurus = . . .?
Jawab :
y = mx
y = -4 / 5 x
-4y = 5x
-4y -5y = 0
<-> 4y + 5y = 0
[/su_box]
[su_box title=”Contoh Soal 5″ box_color=”#0031e8″]
Persamaan garis lurus yang melalui titik ( 0 , -2 ) dan m = 3/4 adalah . . .?
Penyelesaian :
Diketahui :
Titik garis ( 0 , -2 )
m = 3 / 4
Ditanya : Persamaan garis = . . .?
Jawab :
Cara 1
y = mx + c
y = 3/4 x + ( -2 ) x4
< => 4y = 3x – 8
< = > -3x + 4y + 8 = 0
Cara 2
y – y1 = m ( x – x1 )
y – ( -2 ) = 3/4 ( x – 0 )
y + 2 = 3/4 x x4
< = > 4y + 8 = 3x
< = > -3y + 4y + 8
[/su_box]
[su_box title=”Contoh Soal 6″ box_color=”#0031e8″]
Tentukan persamaan garis G yang melalui garis ( 0 , 4 ) dan sejajar dengan garis H yang melalui titik pusat koordinat dan titik ( 3 ,2 ) ?
Penyelesaian :
Diketahui :
Titik koordinat ( 0 , 0 ) dan titik ( 3 , 2 )
Ditanya : Persamaan garis G = . . .?
Jawab :
Langkah pertama kita tentukan gradiennya terlebih dahulu , yaitu :
m = y2 – y1 / x2 – x1
m = 2 – 0 / 3 – 0
m = 2/ 3
Karena Garis G // H , maka gradiennya adalah 2/3 DAN Melalui titik ( 0 , 4 ) , maka persamaan garisnya adalah :
y = mx + c
y = 2 / 3 x + 4 x3
< = >3y = 2x + 12
< = > 3y – 2x – 12 = 0
< = > 2x – 3y + 12 = 0
[/su_box]
[su_box title=”Contoh Soal 7″ box_color=”#0031e8″]
Tentukan persamaan garis Z yang melalui titik ( 4 , 5 ) dan ( -5 , 3 ) ?
Penyelesaian :
Diketahui :
Titik A ( 4 , 5 )
Titik B ( -5 , 3 )
Ditanya : Persamaan garis Z = . . .?
Jawab :
Cara 1
Langkah pertama yaitu mencari gradien terlebih dahulu :
m = y1 – y2 / x1 – x2
m = 5 – 3 / 4 – ( -5 )
m = 2 / 9
Selanjutnya yaitu memasukkan ke dalam rumus :
Persamaan garis melalui titik ( 4 , 5 ) dan bergradien 2 / 9
y – y1 = m ( x – x1 )
y – 5 = 2/9 ( x – 4 )
y – 5 = 2/9x – 8/ 9
y = 2/9 x – 8 / 9 + 5
y = 2/9 x – 8/9 + 45 /9
y = 2/9x – 37 / 9
Cara 2
Tanpa mencari gradien, yaitu dengan cara
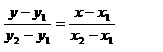
y – 5 / 3 – 5 = x – 4 / -5 – 4
y – 5 / -2 = x – 4 / -9
-9 ( y – 5 ) = -2 ( x – 4 )
-9y + 45 = -2x + 8
-9y + 2x +45 – 8 = 0
2x – 9y + 37 : 9
< = > 2/9 x – y + 37 / 9
< = > y = 2/9x + 37 / 9
[/su_box]
Demikian penjelasan mengenai rumus persamaan garis lurus dan beberapa contohnya . Semoga dengan penjelasan di atas, sedikit membantu memecahkan permasalahan dalam mengerjakan soal yang berhubungan dengan menentukan garis lurus .
Inti dari materi ini adalah memahami apa itu gradien dan memahami antara titik yang dilalui baik titik pusat koordinat , titik koordinat y ataupun titik koordinat x. Atau jika dilambangkan yaitu titik pusat koordint ( 0 , 0 ) , titik koordinat ( x1 , y1 ) dan ( x2 , y 2 ).
Semoga bermanfaat . . . .