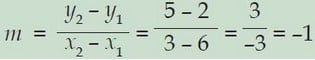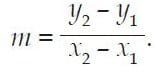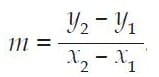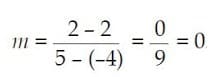Rumus Gradien adalah rumus yang di pakai untuk mengukur pada kemiringan suatu garis, Berikut ini akan kami jelaskan lengkap mengenai rumus gradien yang meliputi pengertian, rumus dan contoh soalnya
Gradien disebut juga sebagai koefisien arah pada garis lurus dan dilambangkan huruf m.. Untuk lebih jelasnya simak pembahasan di bawah ini

Gradien adalah nilai kemiringan pada suatu garis yang membandingkan antara komponen Y dengan komponen X
Rumus Mencari Gradien
Terdapat beberapa kondisi ataupun keadaan untuk mencari gradien garis, perhatika pembahasa berikut ini
1. Gradien Garis Melalui Titik Pusat (0,0) dan Titik (x, y)
Diketahui bahwa persamaan garis yang melalui titik pusat (0,0) dan titik (x, y) adalah
y = mx.
Perhatikan contoh berikut ini.
Mari kita bahas dengan soal dan pembahasannya
Tentukanlah gradien persamaan garis melalui titik pusat dan titik (3, 5)!
Penyelesaian:
Persamaan garis melalui titik (0, 0) dan (3, 5) adalah y = (5/3)x.
Hingga gradiennya yaitu 5/3.
Dari contoh soal tersebut bisa kita simpulkan bahwa gradien dari persaman garis y = mx adalah m.
Kesimpulan perbandingan antara komponen y dengan komponen x pada tiap ruas garis adalah sama. Nilai perbandingan itu dinamakan gradien.
Maka, persamaan garis y = mx mempunyai gradien m dengan m = y/x.
2. Gradien Garis Melalui Dua Buah Titik (x1, y1) dan (x2, y2)
Tidak selalu bahwa sebuah garis tersebut melewati titik pusat (0,0). Jika suatu garis tidak melalui titik pusat (0,0), dapatkah kamu menentukan gradiennya?
Mari kita bahas contoh soal dan pembahasannya
Tentukanlah gradien persamaan garis melalui titik (6, 2) dan titik (3, 5)!
Penyelesaian:
x1 = 6; y1 = 2; x2 = 3; y2 = 5
Jadi, gradien persamaan garisnya adalah -1.
Kesimpulan perbandingan komponen x dan komponen y untuk setiap ruas garis yaitu sama, yaitu 1. Bilangan 1 ini adalah gradien dari persamaan garis y = x + 2.
Maka, persaman garis y = mx, c ≠ 0 mempunyai gradien m dengan;
3. Gradien Garis Sejajar Sumbu-x dan Sumbu-y
Untuk mencari gradien garis yang sejajar sumbu-x dan gradien garis yang sejajar sumbu-y bisa memakai rumus berikut
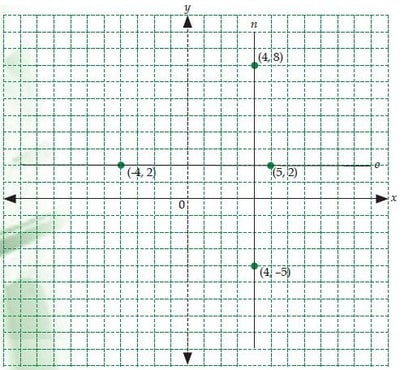
Perhatikan gambar berikut ini
Garis o sejajar dengan sumbu-x dan garis n sejajar dengan sumbu-y.
Pada gambar tersebut terlihat jelas bahwa garis o melalui titik (-4, 2) dan (5, 2). Gradien garis o yaitu
Maka, gradien garis sejajar sumbu-x adalah 0.
Perhatikan garis n di bawah ini!
Garis n melalui titik (4, 8) dan (4, -5).
Gradien garis n yaitu m = (–5 – 8):(4 – 4) = 13/0 = (tidak didefinisikan).
Maka, gradien garis sejajar sumbu-y tidak didefinisikan.
4. Gradien Garis Yang Saling Sejajar
Gradien garis sejajar sumbu-x yaitu 0. Bagaimana dengan gradien dengan dua buah garis yang sejajar seperti terlihat pada gambar berikut?
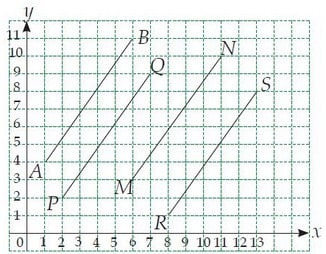
Perhatikan gambar tersebut, lalu kemudian lakukan kegiatan di bawah ini guna mencari gradien garis yang sejajar. Apa yang bisa di simpulkan berdasarkan kegiatan itu ?
Carilah gradien ruas garis AB, PQ, MN, dan RS pada gambar tersebut dengan melengkapi titik-titik berikut ini!
• Titik A (1, 4) ; B (6, 11)
Gradien AB = (11 – 4):(6 – 1) = 7/5
• Titik P (2,2) ; Q (7,9)
Gradien PQ = (9 – 2):(7 – 2) = 7/5
• Titik M (6,3); N (11,10)
Gradien MN = (10 – 3):(11–6) = 7/5
• Titik R (1,4); S (6,11)
Gradien RS = (11 – 7):(6 – 1) = 7/5
Maka, gradien garis AB = PQ = MN = RS = 7/5 .
5. Gradien Garis Saling Tegak Lurus
Selain kedudukan 2 buah garis sejajar, ada juga kedudukan 2 garis yang saling tegak lurus. Bagaimana gradien garis yang tegak lurus? Apakah gradiennya sama?
Gradien 2 buah garis yang tegak lurus jika dikalikan hasilnya sama dengan –1.
Maka, jika l adalah sebuah garis tegak lurus dengan garis p maka berlaku ml × mp = –1.
Contoh Soal
Untuk memudahkan dala pemahaman, sima beberapa contoh soal dibawah ini
Soal No.1
Tentukanlah gradien dari persamaan garis berikut ini:
a) y = 3x + 2
b) 10x − 6y + 3 = 0
Jawab :
a) y = 3x + 2
Pola persamaan garis pada soal a adalah y = mx + C
Hingga mudah menemukan gradien garisnya m = 3
b) 18x − 6y + 24 = 0
Ubah persamaan b jadi pola y = mx + c
18x − 6y + 24 = 0
18x + 24 = 6y
6y = 18x + 24
bagi dengan 6
y = 3x + 4
hingga m = 3
Soal No. 2
Tentukanlah persamaan garis melalui titik (3, 1) dan tegak lurus dengan garis y = 2x + 5
Jawab :
2 garis saling tegak lurus jika memenuhi syarat maka sebagai berikut
m1 ⋅ m2 = −1
y = 2x + 5 mempunyai gradien m1 = 2, hingga garis yang dicari persamaannya harus mempunyai gradien
m1 ⋅ m2 = −1
2 ⋅ m2 = −1
m2 = − 1/2
Susun persamaan garisnya
y − y1 = m(x − x1)
y − 1 = 1/2(x − 3)
y − 1 = 1/2 x − 3/2
y = 1/2 x − 3/2 + 1
y = 1/2 x − 1/2
Soal No. 3
Tentukanlah persamaan garis yang melewati titik (3, 1) dan sejajar garis y = 2x + 5
Jawab :
2 garis yang sejajar mempunyai syarat gradiennya harus sama atau
m1 = m2
Gradien garis y = 2x + 5 yaitu 2
Hingga gradien garis yang dicari juga 2 sebab mereka sejajar.
Hingga y − y1 = m(x − x1)
y − 1 = 2 (x − 3)
= 2x − 6
y = 2x − 6 + 1
y = 2x − 5
Soal No. 4
Garis p mempunyai persamaan :
y = 2x + 5
Tentukanlah persamaan garis yang didapat dengan:
a) menggeser garis p keatas sebanyak 3 satuan
b) menggeser garis p kebawah sebanyak 3 satuan
Jawab :
Pergeseran garis ke atas dan ke bawah.
y = 2x + 5
a) digeser keatas 3 satuan menjadi:
y = 2x + 5 + 3
y = 2x + 8
b) digeser kebawah 3 satuan
y = 2x + 5 − 3
y = 2x + 2
Soal No. 5
Garis m mempunyai persamaan :
y = 2x + 10
Tentukanlah persamaan garis yang didapatkan
a) menggeser garis m ke arah kanan sebanyak 3 satuan
b) menggeser garis m ke arah kiri sebanyak 3 satuan
Jawab :
Pergeseran garis ke kanan dan ke kiri.
y = 2x + 10
a) digeser ke kanan 3 satuan
y = 2(x − 3) + 10
y = 2x − 6 + 10
y = 2x + 4
b) digeser ke kiri 3 satuan
y = 2(x + 3) + 10
y = 2x + 6 + 10
y = 2x + 16
Demikianlah pembahasan mengenai gradien, Semoga bermanfaat
Artikel Terkait :