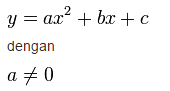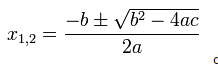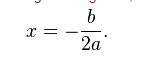Rumus Persamaan Kuadrat | Rumus persamaan kuadrat merupakan rumus untuk menyelesaikan suatu bentuk persamaan kuadrat . Bagaimanakah cara untuk menyelesaikannya ? Sebelum mengetahui bagaimana cara untuk menyelesaikannya , kita harus mengetahui terlebih dahulu mengenai pengertian persamaan kuadrat .
Persamaan Kadrat adalah Suatu bentuk persamaan polinomial berpangkat dua .
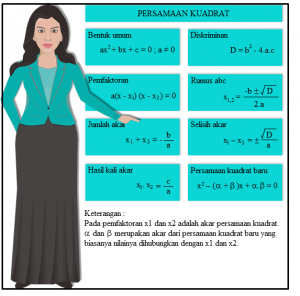
Bentuk umum persamaan kuadrat :
Keterangan :
a = koefisien kuadrat x
b = koefisisen linier x
c = suku bebas atau koefisien konstanta
Nilai koefisien a , b , dan c dalam Fungsi persamaan kuadrat :
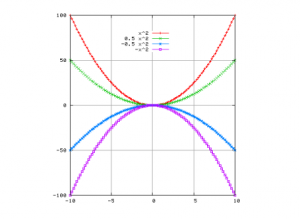
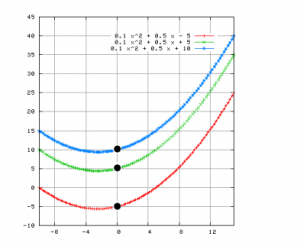
- Koefisien a , menentukan seberapa cekung atau cembung suatu parabola dalam fungsi persamaan kuadrat . Apabila a > 0 , maka parabola tersebut membuka ke atas . Dan apabila a < 0 , maka parabola akan terbuka ke bawah .
Perhatikan gambar di bawah ini :
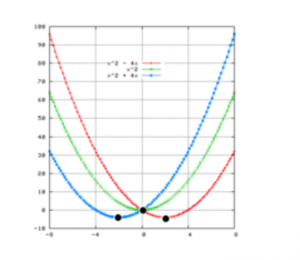
- Koefisien b , Menentukan posisi puncak x atau sumbu simetri dari sebuah kurva yang dibentuk . Posisi tepatnya yaitu – b / 2a
Perhatikan Gambar di bawah ini :
- KOefisien c , menentukan titik potong dari suatu bentuk persamaan dalam bentuk parabola yang dibentuk pada sumbu y , dimana x = 0
Perhatikan gambar di bawah ini :
Rumus Persamaan Kuadrat
Rumus persamaan kuadrat merupakan suatu cra untuk menyelesaikan sebuah permasalahan persamaan kuadrat . Berikut adalah Cara – cara untuk menyelesaikan persamaan kuadrat :
- Memfaktorkan
Memfaktorkan yaitu cara menyelesaikan persamaan kuadrat dengan cara mencari 2 bilangan yang merupakan faktor dari bentuk persamaaan tersebut . Bentuk umum dari persamaan kuadrat ax2 + bx + c = 0 , dengan a≠0
<=> ( x – a ) ( x – b ) atau ( x – a ) ( x + b )
Caranya yaitu mencari 2 angka yang apabila di jumlahkan hasilnya b , dan apabila dikalikan hasilnya c .
Contoh :
Tentukan himpunan penyelesaian dari bentuk persamaan x2 – 2x – 8 = 0
Penyelesaian:
x2 – 2x – 8 = 0 , faktor dari persamaan tersebut adalah ( 2 , -4 )
x2 – 2x – 8 = 0
< = > ( x + 2 ) ( x -4 )
Jadi HP = { 2 , -4 }
2. Melengkapi Kuadrat Sempurna
Langkah – langkah dalam melengkapi kuadrat menjadi bentuk kuadrat sempurna :
a. Koefisien x2 harus 1
b. Konstanta pindah ke ruas kanan
c. Di ubah kebentuk kuadrat sempurna
Contoh :
Tentukan himpunan penyelesaian dari bentuk persamaan x2 – 2x – 8 = 0
Penyelesaian :
x2 + 2x – 8 = 0
<= > x2 + 2x = 8 , memindahkan kontanta ke sebelah kanan , setelah itu mencari 1/2 dari konstanta untuk menjadikan kuadrat menjadi sempurna .
< => x2 + 2x + ( 1/2 .2 )2 = 8 + ( 1/2 .2 )2
<= > x2 + 2x + 1 = 8 + 1
< = > x2 + 2x + 1= 8 + 1
< = > x2 + 2x + 1= 9
< = > ( x + 1 ) 2 = 9
<=> x + 1 = ± √9
< => x + 1 = ± 3
< = > x + 1 = 3 , atau x + 1 = – 3
< = > x = 3 – 1 , x = -3 -1
< = > x = 2 , x = -4
Maka HP = { 2 , -4 }
3. Menggunakan Rumus ABC ( Rumus Kuadratis )
Contoh :
Tentukan himpunan penyelesaian dari bentuk persamaan x2 – 2x – 8 = 0
Penyelesaian :
x2 – 2x – 8 = 0 , lalu menuliskan rumus abc
<=>x1 ,2 = – b ± √b2 – 4ac / 2.a
<=>x1 ,2 = 2 ± √4 + 32 /2
<=>x1 ,2 = 2 ± 6 /2
<=> x1,2 = (2+6)/2 atau x1,2 = (2-6)/2
<=> x1 = 4 , atau x2 = -2
Jadi HP = { 4 , -2 }
Mengapa di sebut dengan rumus abc ? Karena rumus tersebut digunakan untuk menghitung akar – akar dari a,b dan c . Dalam rumus abc ini , terdapat sebuah istilah yaitu diskriminan atau determinan . Diskriminan atau determinan memiliki arti tanda akar b²-4ac , atau dilambangkan dengan huruf ” D ” .
Suatu koefisien riil dalam persamaan kuadrat ,dapat hanya memiliki satu akar atau dua akar yang berbeda dan akar – akar tersebut dapat berbentuk bilangan riil atau kompleks . Diskriminan , dapat menentukan jumlah banyaknya akar dari persamaan tersebut . Berikut adalah kemungkinan – kemungkinan yang dapat terjadi :
- Apabila diskriminan bernilai positif , maka akan terdapat dua akar yang berbeda dan merupakan bilangan riil . Dan apabila koefisien dalam persamaan tersebutmerupakan bilangan bulat , dan diskriminan nya berupa bilangan kuadrat sempurna , maka akar – akar dari persamaan tersebut berupa bilangan rasional atau bisa juga berupa bilangan irasional .
- Apabila diskriminan dari persamaan tersebut bernilai nol , maka akarnya berupa satu bilangan riil .Dan di sebut sebagai akar ganda ,
akar ganda , yaitu :
- Apabila diskriminan bernilai negatif dan tidak terdapat bilangan riil . Sebagai gantinya , terdapat dua buah akar kompleks yang disebut juga sebagai konjugat kompleks. Berikut adalah bentuk dari konjugat kompleks:
Rumus Yang perlu untuk difahami dan Diingat dalam Persamaan Kuadrat :
1. Bentuk Umum persamaan Kuadrat :
ax2 + bx + c = 0 , dengan a≠0
2. Pemfaktoran
( x – x1 ) ( x – x2 ) = 0
3. Jumlah Akar
x1 + x2 = -b / a
4. Hasil kali akar
x1 . x2 = c / a
5. Selisih akar
x1 – x2 = ± √D /4
6. Diskriminan
D = b2 – 2a.c
7. Rumus ABC
x1 , 2 = – b ± √D / 2.a
8. Persamaan Kuadrat Baru
x2 – ( a +β ) x + a . β = 0
Demikian penjelasan mengenai rumus persamaan kuadrat . Pada dasarnya , operasi hitung yang dipakai dalam persamaan kuadrat yaitu sama dengan operasi hitung matematika yang lainnya yaitu mengenai penjumlahan , pengurangan , perkalian dan pembagian . Serta kita juga harus faham inti dasar dari persamaan kuadrat tersebut , serta tidak lupa untuk sering – sering latihan mengerjakan soal – soal yang berhubungan dengan persamaan kuadrat. Inti dasar dari persamaan kuadrat adalah , memahami bahwa bentuk persamaan kuadrat secara umum adalah ax2 + bx + c = 0 dimana a bukan 0 . Semoga dapat sedikit menambah pengetahuan mengenai rumus persamaan kuadrat .