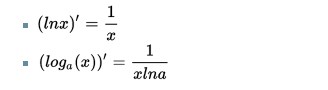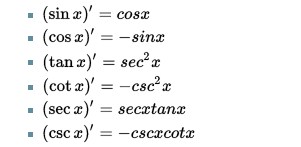Rumus Turunan Matematika – Pembahasan tentang Rumus Matematika Turunan ini merupakan salah satu Pelajaran Matematika yang ada di tingkat SMA (Sekolah Menengah Atas) dan tidak bisa dipungkiri bahwa Soal – Soal tentang Turunan Matematika sering muncul di Soal – Soal Ujian baik itu Ujian Sekolah maupun Ujian Nasional. Untuk itu sudah sangat bijak sekali bagi kalian para Pelajar SMA untuk bisa memahami dan mengenal Rumus Turunan (Diferensial) Matematika ini, setidaknya agar kalian bisa mengerjakan Soal Turunan Matematika yang muncul di Ujian Sekolah dan Ujian Nasional.
Oleh karena itu di kesempatan ini saya selaku pemilik Blog Rumus Rumus akan mencoba untuk menjelaskan secara lebih detail tentang Materi Rumus Diferensial Matematika kepada kalian para pembaca baik itu para Pelajar SMA, Mahasiswa dan Masyarakat Umum. Hal tersebut dikarenakan di Jaman Teknologi yang sudah semakin Maju khususnya Internet, kalian sebagai Pelajar sudah bisa belajar tidak hanya di Sekolah tetapi bisa di Internet karena Google sebagai Mesin Pencari Terbesar sudah menyediakan berbagai Informasi – Informasi dan Ilmu yang bisa dibaca dan dipelajari oleh semua Kalangan, termasuk kalian sebagai pelajar.
Langsung saja untuk Pengertian Turunan Matematika adalah pengukuran terhadap Fungsi yang berubah seiring perubahan Nilai Inputnya karena secara umum Turunan Matematika itu menyatakan bagaimana suatu besaran dapat berubah akibat perubahan besaran lainnya. Sebagai Contoh, Turunan dari Posisi sebuah benda yang bergerak terhadap waktu ialah Kecepatan yang sesaat dari Objek tersebut dan proses dlm menemukan Turunan disebut dengan Diferensiasi.
Mungkin bisa kalian langsung lihat penjelasan tentang Rumus Diferensial Matematika beserta Contoh Soal Turunan Matematika dan yang perlu ditekankan oleh kalian sebagai pembaca dan pelajar tingkat Sekolah Menengah Atas (SMA) bahwa didalam Rumus Matematika Turunan terbagi menjadi beberapa Rumus yang antara lain Rumus Turunan Dasar, Rumus Turunan Eksponen dan Bilangan Natural, Rumus Turunan Trigonometri, Rumus Turunan Logaritma dan Bilangan Natural.
Rumus Turunan Matematika Dasar
Rumus Turunan Eksponen dan Bilangan Natural
Rumus Turunan Logaritma dan Bilangan Natural
Rumus Turunan Trigonometri
Contoh Soal Turunan Matematika
1. Contoh Soal Turunan Matematika dengan menentukan Gradien pada Garis Singgung Kurva dan contohnya seperti ini : ” Tentukan nilai Gradien pada Garis Singgung dari Kurva sebesar y = x² + 3x pada titik (1, -4) ??
Jawabannya :
y = x² + 3x maka y = 2x + 3
m = y (1) = 2 x 1 + 3
= 5
2. Lalu didalam Contoh Soal Turunan Matematika didalam Fungsi Trigonometri bisa kalian lihat contohnya seperti ini : ” Jika y = x² Sin2x, maka dy/dx = ?
Jawabannya :
y = x² Sin2x
Misalkan :
u (x) = x² maka u’ (x) = 2x
v (x) = Sin2x maka v'(x) = 2Cos2x
y = u (x). v(x)
y’ (x) = u'(x) v(x) + u(x) v'(x)
= 2x (Sin2x) + x² (2Cos2x)
= 2xSin2x + 2x²Cos2x.
Itulah pembahasan mengenai Macam – Macam Rumus Diferensial dan Contoh Soal Turunan Matematikannya yang bisa Penulis sampaikan kepada kalian sebagai para pembaca di Blog Rumus Rumus ini dan sebagai informasi saja bahwa pembahasan tentang Turunan (Diferensial) Matematika diatas telah kami buat dengan Referensi Buku Pelajaran Matematika SMA dan telah ditinjau ulang di Wikipedia sehingga pembahasan Rumus Diferensial (Turunan) ini sudah bisa menjadi pedoman kalian untuk lebih mengenal tentang Turunan Matematika.
Semoga saja ulasan ini bisa berguna dan bermanfaat bagi kalian Para Pembaca dan Para Pelajar Sekolah Menengah Atas (SMA) karena sekali lagi bisa ditekankan disini bahwa Materi Pelajaran Matematika Turunan ini merupakan salah satu Materi Matematika yang sering muncul di Soal Ujian baik itu Ujian Akhir Sekolah (UAS) SMA dan Ujian Nasional (UN) SMA sehingga sudah sangat tepat sekali bagi kalian Para Pelajar untuk lebih mempelajari dan memahami Materi Turunan Matematika ini. Selain itu sebagai tambahan informasi saja bahwa jika kalian sebagai Pembaca dan Pelajar ingin mengenal lebih dalam mengenai Materi Rumus Trigonometri Matematika bisa kalian langsung menuju ketautan tersebut karena disitu telah dibahas secara lebih detail mengenal Trigonometri Matematika.