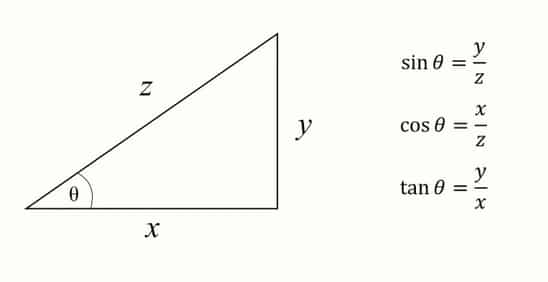Tabel Sin Cos Tan Dari 0 Sampai 360 Derajat Terlengkap

Tabel Sin Cos Tan – Sahabat Rumus Rumus setelah dipertemuan sebelumnya telah saya bahas tentang rumus dan fungsi trigonometri secara lebih detail dan lengkap, maka dipertemuan sekarang ini saya akan mencoba memberikan ulasan kepada kalian para pembaca tentang tabel sin cos tan dari 0 derajat sampai 360 derajat.

Karena tidak bisa dipungkiri bahwa sin cos tan ini merupakan salah satu fungsi trigonometri itu sendiri sehingga bisa dikatakan bahwa trigonometri sangat berkaitan dengan sin cos tan.

Fungsi trigonometri seperti sin cos dan tan ini sangat membantu untuk kalian dalam menghitung perhitungan sudut bangun terutama didalam perhitungan sudut istimewa trigonometri dasar.

Oleh karena itu sudah sangat bijak sekali bagi kalian para pelajar siswa dan siswi khususnya tingkat sekolah menengah atas (SMA) untuk lebih mengetahui dan lebih mengenal tentang nilai sin cos tan dalam sudut istimewa trigonometri karena nilai sin cos dan tan ini sering muncul di soal – soal ujian, termasuk juga keluar di soal ujian nasional (UN) tingkat SMA.

Dengan adanya tabel trigonometri ini maka akan sangat membantu dalam mengerjakan nilai trigonometri dalam sebuah sudut.

Nilai trigonometri yang akan dijabarkan ini ialah sinus, cosinus, dan juga tangen. Yang biasa disebut juga dengan singkatan sin cos tan.

Pengertian Sin Cos Tan

Sebelum memahami ke tabel nilai cos sin tan trigonometri, lebih baiknya pahamlah terlebih dahulu dengan pengertian atau istilah sin cos tan dan trigonometri

• Sin (sinus) ialah perbandingan panjang sebuah segitiga yakni antara sisi depan sudut dengan sisi miring segitiga, y/z.
• Cos (cosinus) ialah perbandingan panjang sebuah segitiga yakni antara sisi samping sudut dengan sisi miringnya, x/z.
• Tan (tangen) ialah perbandingan panjang sebuah segitiga antara sisi depan sudut dan sisi samping segitiga, y/x.
• Trigonometri adalah salah satu cabang dari ilmu matematika yang membahas tentang hubungan antara panjang dan sudut pada sebuah segitiga.

Untuk lebih jelasnya tentan penjelasan diatas, lihatlah gambar dibawah ini :

Catatan : Seluruh perbandingan trigonometri sin cos tan diatas terbatas yakni hanya berlaku untuk objek segitiga siku siku atau segitiga dimana salah satu sudutnya nilainya 90 derajat.

Tabel Sin Cos Tan

Untuk itu dibawah ini telah kami buatkan tabel cos sin tan seluruh sudut yang terbentuk dalam satu lingkaran penuh atau yang sering disebut dengan lingkaran 360 derajat. 

Rumus sin cos tan sudut istimewa sampai 360 didalam tabel tersebut sangat berguna bagi kalian untuk mempermudah dalam menjawab pertanyaan – pertanyaan terkait rumus dan persamaan trigonometri, langsung saja dibawah ini tabel sinus cosinus tangen dalam sudut istimewa trigonometri yang terbagi menjadi 4 kuadran.

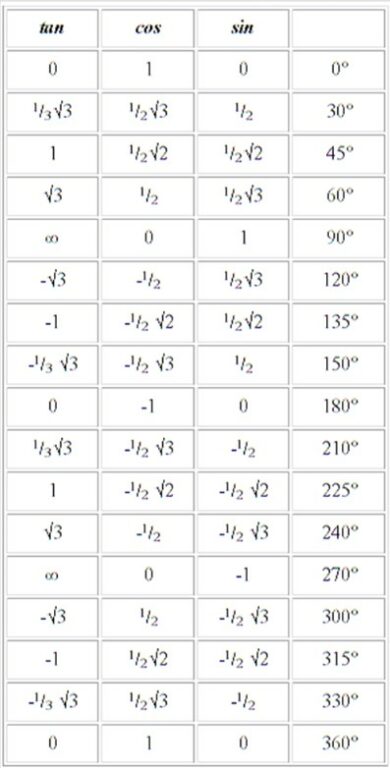
Tabel Sin Cos Tan Kuadran 1 dari 0º sampai 90º

	0 derajat	30 derajat	45 derajat	60 derajat	90 derajat
Sin	0	½	½√2	½√3	1
Cos	1	½√3	½√2	½	0
Tan	0	½√3	1	√3	∞

Tabel Sin Cos Tan Kuadran 2 dari 90º sampai 180º

	90 derajat	120 derajat	135 derajat	150 derajat	180 derajat
Sin	1	½√3	½√2	½	0
Cos	0	-½	-½√2	-½√3	-1
Tan	∞	-√3	-1	-½√3	0

Tabel Sin Cos Tan Kuadran 3 dari 180º sampai 270º

	180 derajat	210 derajat	225 derajat	240 derajat	270 derajat
Sin	0	-½	-½√2	-½√3	-1
Cos	-1	-½√3	-½√2	-½	0
Tan	0	1/3√3	1	√3	∞

Tabel Sin Cos Tan Kuadran 4 dari 270º sampai 360º

	270 derajat	300 derajat	315 derajat	330 derajat	360 derajat
Sin	-1	-½√3	-½√2	-½	0
Cos	0	½	½√2	½√3	1
Tan	∞	-√3	-1	-1/3√3	0

Itulah tabel sin cos tan trigonometri didalam ilmu matematika untuk tingkat sekolah menengah atas (SMA) dan semoga saja ulasan tentang sin cos tan trigonometri ini bisa berguna dan bisa memudahkan kalian dalam menghitung perhitungan sudut bangun terutama sudut istimewa trigonometri.

Tabel Sin Cos Tan Sudut Istimewa

Jika penjelasan pada tabel diatas dijelaskan secara 4 kuadran maka jika digabungkan untuk anda bisa download tabel sin cos tan rumus ini di hp atau komputer kalian masing – masing maka rumusrumus.com telah menyediakannya dari hasil gabungan tabel yang dijelaskan diatas, berikut nilai lengkap dari tabel sin cos tan sudut istimewa

Dan mungkin sebatas tambahan informasi saja kepada kalian bahwa pengertian sinus (sin) didalam ilmu matematika menurut wikipedia adalah perbandingan antara sisi segitiga yang ada didepan sudut dengan sisi miring, tetapi dengan catatan bahwa segitiga tersebut adalah sebuah segitiga siku – siku ataupun salah satu sudut segitiga itu mempunyai nilai 90 derajat.

Untuk Pengertian cosinus (cos) didalam ilmu matematika menurut wikipedia adalah suatu perbandingan sisi segitiga yang terletak didalam sudut dengan sisi yang miring, dengan catatan bahwa segitiga tersebut merupakan segitiga adalah segitiga siku – siku ataupun salah satu sudut segitiga itu mempunyai nilai 90 derajat.

Sedangkan untuk pengertian tangen didalam ilmu matematika menurut wikipedia suatu perbandingan sisi segitiga yang ada didepan sudut tersebut dengan sisi segitiga yang terletak di sudut, dengan catatan bahwa segitiga tersebut merupakan segitiga adalah segitiga siku – siku ataupun salah satu sudut segitiga itu mempunyai nilai 90 derajat.

Tabel Trigonometri Untuk Seluruh Sudut

Jika tabel diatas menjelaskan cara menghitung sin cos tan dengan tabel trigonometri sudut istimewa yakni sudut sudut istimewa seperti 0°, 30°, 45°, 60°, dan 90° sehingga akan membantu kalian menghafal dengan cepat nilai sin cos tan dari tabel trigonometri diatas, maka disini akan dijelaskan secara lengkap dan detail tentang nilai sin cos tan untuk seluruh sudut mulai dari 0° sampai 360° sehingga dengan angka pada nilai dibawah ini menjadi cara cepat anda untuk menemukan nilai sin cos tan dengan tepat dan efektif.

Tabel Trigonometri Sudut 0° sampai 90°

Sudut	Radian	Sin	Cos	Tan
0°	0	0	1	0
1°	0.01746	0.01746	0.99985	0.01746
2°	0.03492	0.03491	0.99939	0.03494
3°	0.05238	0.05236	0.99863	0.05243
4°	0.06984	0.06979	0.99756	0.06996
5°	0.0873	0.08719	0.99619	0.08752
6°	0.10476	0.10457	0.99452	0.10515
7°	0.12222	0.12192	0.99254	0.12283
8°	0.13968	0.13923	0.99026	0.1406
9°	0.15714	0.1565	0.98768	0.15845
10°	0.1746	0.17372	0.9848	0.1764
11°	0.19206	0.19089	0.98161	0.19446
12°	0.20952	0.20799	0.97813	0.21265
13°	0.22698	0.22504	0.97435	0.23096
14°	0.24444	0.24202	0.97027	0.24943
15°	0.26191	0.25892	0.9659	0.26806
16°	0.27937	0.27575	0.96123	0.28687
17°	0.29683	0.29249	0.95627	0.30586
18°	0.31429	0.30914	0.95102	0.32506
19°	0.33175	0.32569	0.94548	0.34448
20°	0.34921	0.34215	0.93965	0.36413
21°	0.36667	0.35851	0.93353	0.38403
22°	0.38413	0.37475	0.92713	0.40421
23°	0.40159	0.39088	0.92044	0.42467
24°	0.41905	0.40689	0.91348	0.44543
25°	0.43651	0.42278	0.90623	0.46652
26°	0.45397	0.43854	0.89871	0.48796
27°	0.47143	0.45416	0.89092	0.50976
28°	0.48889	0.46965	0.88286	0.53196
29°	0.50635	0.48499	0.87452	0.55458
30°	0.52381	0.50018	0.86592	0.57763
31°	0.54127	0.51523	0.85706	0.60116
32°	0.55873	0.53011	0.84793	0.62518
33°	0.57619	0.54483	0.83854	0.64974
34°	0.59365	0.55939	0.8289	0.67486
35°	0.61111	0.57378	0.81901	0.70057
36°	0.62857	0.58799	0.80887	0.72693
37°	0.64603	0.60202	0.79848	0.75396
38°	0.66349	0.61587	0.78785	0.78172
39°	0.68095	0.62953	0.77697	0.81024
40°	0.69841	0.643	0.76586	0.83958
41°	0.71587	0.65628	0.75452	0.86979
42°	0.73333	0.66935	0.74295	0.90094
43°	0.75079	0.68222	0.73115	0.93308
44°	0.76825	0.69488	0.71913	0.96629
45°	0.78571	0.70733	0.70688	1.00063
46°	0.80318	0.71956	0.69443	1.0362
47°	0.82064	0.73158	0.68176	1.07308
48°	0.8381	0.74337	0.66888	1.11137
49°	0.85556	0.75494	0.6558	1.15117
50°	0.87302	0.76627	0.64252	1.1926
51°	0.89048	0.77737	0.62904	1.2358
52°	0.90794	0.78824	0.61537	1.28091
53°	0.9254	0.79886	0.60152	1.32807
54°	0.94286	0.80924	0.58748	1.37748
55°	0.96032	0.81937	0.57326	1.42932
56°	0.97778	0.82926	0.55887	1.48382
57°	0.99524	0.83889	0.5443	1.54122
58°	1.0127	0.84826	0.52957	1.60179
59°	1.03016	0.85738	0.51468	1.66584
60°	1.04762	0.86624	0.49964	1.73374
61°	1.06508	0.87483	0.48444	1.80587
62°	1.08254	0.88315	0.46909	1.8827
63°	1.1	0.89121	0.4536	1.96476
64°	1.11746	0.89899	0.43797	2.05265
65°	1.13492	0.9065	0.4222	2.14707
66°	1.15238	0.91373	0.40631	2.24884
67°	1.16984	0.92069	0.3903	2.35894
68°	1.1873	0.92736	0.37416	2.4785
69°	1.20476	0.93375	0.35792	2.60887
70°	1.22222	0.93986	0.34156	2.75169
71°	1.23968	0.94568	0.3251	2.90892
72°	1.25714	0.95121	0.30854	3.08299
73°	1.2746	0.95646	0.29188	3.27686
74°	1.29206	0.96141	0.27514	3.49427
75°	1.30952	0.96606	0.25831	3.73993
76°	1.32698	0.97043	0.2414	4.01992
77°	1.34444	0.97449	0.22442	4.34219
78°	1.36191	0.97826	0.20738	4.71734
79°	1.37937	0.98173	0.19026	5.15984
80°	1.39683	0.98491	0.1731	5.68998
81°	1.41429	0.98778	0.15587	6.33709
82°	1.43175	0.99035	0.1386	7.14523
83°	1.44921	0.99262	0.12129	8.18379
84°	1.46667	0.99458	0.10394	9.56868
85°	1.48413	0.99625	0.08656	11.5092
86°	1.50159	0.99761	0.06915	14.4259
87°	1.51905	0.99866	0.05173	19.3069
88°	1.53651	0.99941	0.03428	29.153
89°	1.55397	0.99986	0.01683	59.4189
90°	1.57143	1	0	∞

Tabel Trigonometri Sudut 90° sampai 180°

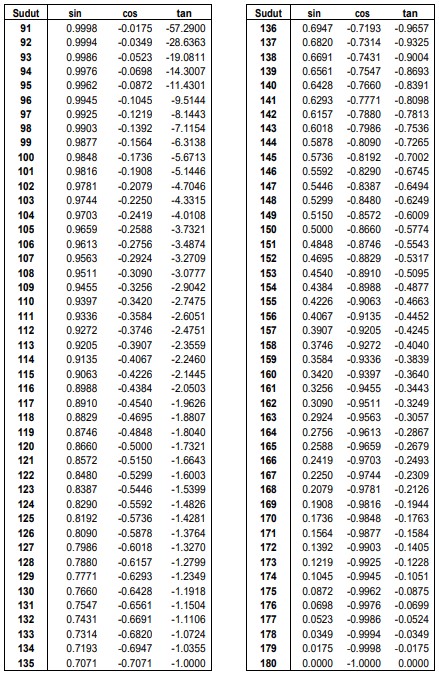
Tabel Trigonometri Sudut 180° sampai 270°

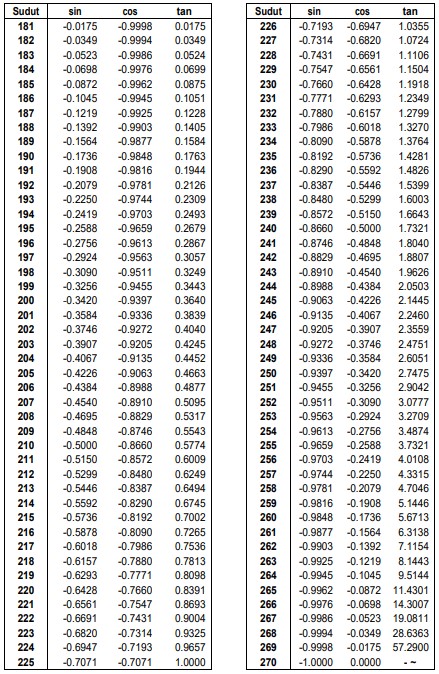
Tabel Trigonometri Sudut 270° sampai 360°

Itulah materi tentang sin cos tan tabel yang dapat diuraikan oleh RumusRumus.com semoga kita dapat memahaminya dengan baik… semoga bermanfaat