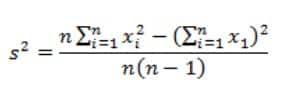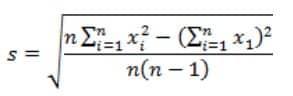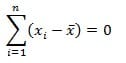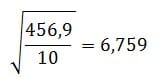Rumusrumus.com kali ini akan membahas tentang standar deviasi yang meliputi pengertian dan cara menghitung standar deviasi baik secara manual maupun menggunakan exel serta beberapa contoh soal agar dpat mudah di pahami, lebih lengkap nya simak uraian dibawah ini
Pengertian
Standar deviasi yaitu nilai statistik yang dimanfaatkan untuk menentukan bagaimana sebaran data dalam sampel, serta seberapa dekat titik data individu ke mean ataupun rata-rata nilai sampel
Cara Menghitung Standar Deviasi
Ada beberapa metode yang bisa dimanfaatkan. Seperti menghitung secara manual, dengan kalkulator maupun Excel.
Secara Manual
Untuk mengetahui cara menghitungnya maka ada dua rumus yang harus diketahui, yakni rumus varian dan rumus standar deviasi. Berikut adalah rumus yang bisa digunakan:
Rumus Varian
Rumus Standar Deviasi
Keterangan:
s2 : Varian
n : Ukuran sampel
s : Standar deviasi
x : Rata-rata
xi : Nilai x ke-i
Cara Menghitung Standar Deviasi di Excel
Rumus untuk menghitung di Excel adalah STDEV. Sebagai gambaran silakan simak contoh di bawah ini.
Contoh :
Berdasarkan sampel nilai ujian mata pelajaran beberapa siswa di SMP rakyat diketahui data sebagai berikut:
80, 60, 80, 90, 70, 80, 95
Hitunglah standar deviasi dari data tersebut.
Buka aplikasi dan masukkan data ke dalam tabel. Contohnya seperti tabel di bawah.
Pada baris bawah merupakan nilai standar deviasi. Caranya yaitu dengan menekan tombol =STDEV(number1; number 2; dst). Berdasarkan contoh di atas, maka format rumusnya yaitu
STDEV(B5:B11)
Secara otomatis akan keluar hasil standar deviasi dari sampel di atas, yakni 11,70. Perlu dicatat, (B5:B11) merupakan cell dari data sampel yang di masukkan di Excel. Jadi bukan merupakan rumus pasti. Karena data sampel pada contoh tersebut berada di cell B5 sampai B11 maka kita masukkan (B5:B11).
Keterangan :
- a. STDEV mengasumsikan bahwa argumen adalah contoh dari populasi. Jika data mewakili seluruh populasi, untuk menghitung deviasi standar menggunakan STDEVP.
- b. Standar deviasi dihitung memakai metode “n-1″ .
- c. Argumen dapat berupa nomor atapun nama, array, atau referensi yang mengandung angka.
- d. Nilai-nilai logis dan representasi teks dari nomor yang di ketik langsung ke daftar argumen akan dihitung.
- e. Jika argumen adalah sebuah array atau referensi, hanya nomor/angka dalam array atau referensi yang akan dihitung. Sel kosong, nilai-nilai logis, teks, atau nilai-nilai kesalahan dalam array atau referensi akan diabaikan.
- f. Argumen yang kesalahan nilai atau teks yang tidak bisa diterjemahkan ke dalam nomor/angka akan menyebabkan kesalahan.
- g. Jika ingin memasukkan nilai-nilai logis dan representasi teks angka dalam referensi sebagai bagian dari perhitungan, gunakan fungsi STDEVA.
Contoh Soal
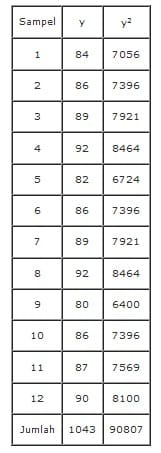
Data umur berbunga (hari) tanaman padi varietas Pandan Wangi yaitu : 84 86 89 92 82 86 89 92 80 86 87 90
Berapakah nilai deviasi dari data tersebut?
Nilai standar deviasi data di atas adalah
Mengitung Standar Deviasi (Simpangan Baku)
Contoh Soal
Selama 10x ula berturut-turut ulangan semester di kampus tercintanya di London, Jonathan mendapat nilai 91, 79, 86, 80, 75, 100, 87, 93, 90,dan 88. Berapa simpangan baku dari nilai ulangan ?
Jawab:
Soal tersebut menanyakan simpangan baku dari data populasi jadi menggunakan rumus simpangan baku untuk populasi.
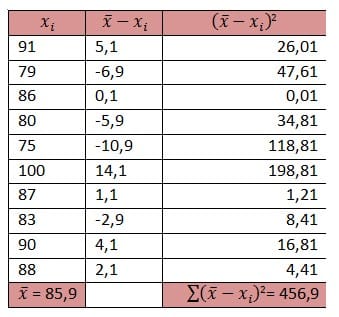
cari dulu rata ratanya
rata-rata = (91+79+86+80+75+100+87+93+90+88)/10 = 859/10 = 85,9
masukan rumus
Dari penghitungan rumus deviasi dari data polulasi di dapatkan hasil
Jika dalam soal menyebutkan sample (bukan populasi) misalnya dari 500 penduduk diambil 150 sample untuk diukur berat badannya… dst, maka menggunakan rumus untuk sample (n-1)
Fungsi Standar Deviasi
Umumnya standar deviasi dimanfaatkan para ahli statistik ataupun orang yang berkecimpung dalam dunia tersebut untuk mengetahui apakah sampel data yang diambil mewakili seluruh populasi.
Karna mencari data yang tepat untuk suatu populasi begitu sulit untuk dilakukan. Maka dari itu perlu menggunakan sampel data yang bisa mewakili seluruh populasi hingga mempermudah untuk melakukan penelitian atau suatu tugas.
Demikianlah penjelasan mengenai standart deviasi yang meliputi cara penyelesaian serta rumusrumusnya, Semoga bermanfaat
Artikel Lainya :