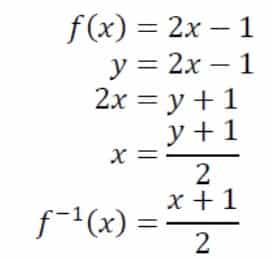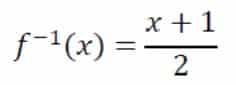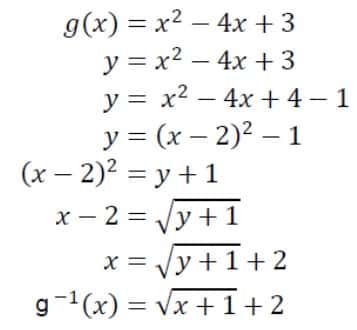Rumus Fungsi Invers

Rumus Fungsi Invers dilambangkan dengan f-1(x). Berikut ini akan kami jelaskan secara lengkap tentang rumus fungsi suatu invers, Untuk lebih jelasnya simak pembahasan di bawah ini

Pengertian Fungsi Invers

Fungsi Invers adalah suatu materi yang erat berkaitan dengan materi fungsi seperti linier, kuadrat, irasional dll. Ada baiknya sebelum belajar jauh tentang invers pahami terlebih dahulu materi fungsi tersebut

Maka, Invers fungsi f bisa di definisika sebagai berikut ini
Jika fungsi f : A —>B dinyatakan sebagai pasangan berurutan

Maka, dari fungsi f adalah f-1 : B—>A ditentukan dengan

Menentukan invers fungsi berarti menukar kedudukan yaitu antara domain dan kodomain.

Apa itu domain dan kodomain?
Domain adalah daerah asal dan kodomain adalah daerah hasil. Sehingga jika diketahui fungsi f memetakan dari A ke B maka invers fungsi dari f memetakan dari B ke A

Simak pembahasan di bawah ini

Diatas menunjukan bahwa contoh menentukan invers pada suatu fungsi yaitu fungsi f(x)=2x-1, sehingga didapatkan invers dari fungsi tersebut yaitu f-1(x)=(x+1)/2

Sebenarnya terdapat cara alternatif yang bisa dikatakan lebih mudah, berikut ini adalah contoh pengerjaan invers memakai cara alternatif dari fungsi f(x)=2x-1

Operasi x untuk fungsi f(x)=2x-1 yaitu :

Dikalikan 2
Dikurangi 1

Kerjakan dengan kebalikan operasi dan urutannya, maka :

Ditambah 1
Dibagi 2

Sehingga inversnya :

Fungsi Invers

Fungsi invers yaitu suatu fungsi kebalikan dari fungsi asalnya. Suatu fungsi f mempunyai fungsi invers (kebalikan) f-1 jika f adalah fungsi satu-satu dan fungsi pada (bijektif). Hubungan itu bisa dinyatakan sebagai berikut:

(f-1)-1 = f

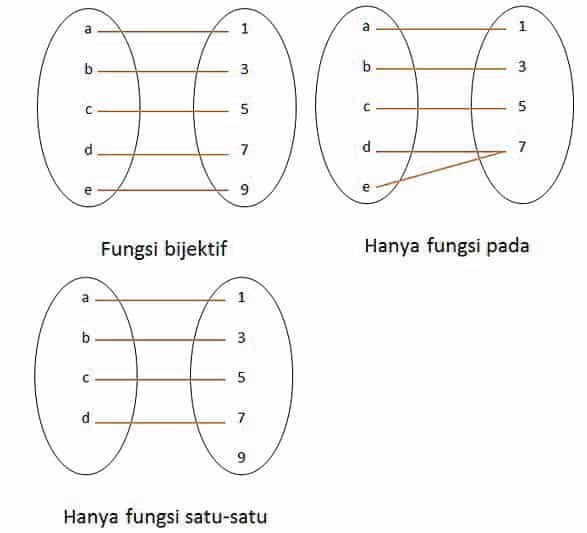
Sederhananya adalah fungsi bijektif terjadi saat jumlah anggota domain = jumlah anggota kodomain. Tidak ada dua atau lebih doamain berbeda yang dipetakan ke kodomain yang sama dan tiap kodomain mempunuyai pasangan di domain, perhatikan gambar berikut ini

Berdasarkan gambar tersebut, pemetaan pertama adalah fungsi bijektif. Pemetaan kedua yaitu bukan fungsi bijektif sebab pemetaan hanya terjadi fungsi pada. Domain d dan e dipetakan dalam anggota kodomain yang sama.

Pemetaan ketiga bukan fungsi bijektif sebab pemetaan itu hanya terjadi fungsi satu-satu. Kodomain 9 tidak mempunyai pasangan pada anggota domain.

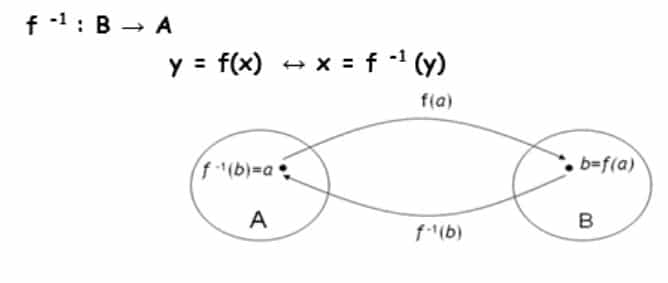
Misalkan f fungsi memetakan x ke y, bisa ditulis y = f(x), maka f-1 yaitu fungsi yang memetakan y ke x, ditulis x = f-1(y). Sebagai contoh misalnya f : A →B fungsi bijektif. Invers fungsi f yaitu fungsi yang mengawankan tiap elemen B dengan tepat satu elemen pada A. Invers fungsi f dinyatakan f-1 seperti di bawah ini:

Contoh Soal

Untuk memudahka dala memahami invers, berikut ini akn kami sajikan berapa contoh soalnya, Simak pembahasan berikut ini

Contoh 1
Jika g(x) = x2 – 4x + 3
tentukanlah g-1(x)!

Penyelesaian :

Cara biasa
Misal g(x) = y

Cara alternatif
Ubah fungsi g(x)=x²-4x+3 hingga menjadi g(x)=(x-2)²-1 dengan cara melengkapkan kuadrat yang sempurna.
operasi pada x dari fungsi g(x)=(x-2)²-1, adalah:

Dikurangi 2
Dikuadratkan
Dikurangi 1

Kerjakan kebalikan operasi dan urutannya :

Ditambah 1
Diakar pangkat dua
Ditambah 2

Hingga inversnya menjadi

Contoh Soal 2
Tentukanlah invers fungsi F(x) = (2x + 2)2 – 5 ?

Cara biasa
Misal F(x) = y
y = (2x + 2)2 – 5
y + 5 = (2x + 2)2
(y + 5)1/2 = 2x + 2
(y + 5)1/2 – 2 = 2x
[(y +5)1/2 – 2]/2 = x

Maka f-1(x) = [(x + 5)1/2 – 2]/2

Cara alternatif
operasi x pada fungsi F(x) = (2x + 2)2 – 5 :

Dikalikan 2
Ditambah 2
Dikuadratkan
Dikurangi 5

kerjakan dengan kebalikan operaasi dan urutannya :

Ditambah 5
Diakar pangkat 2
Dikurangi 2
Dibagi 2

Hasil inversnya adalah f-1(x) = [(x + 5)1/2 – 2]/2

Demikianlah pembahasan kali ini, Semoga bermanfaat

Baca juga :

• Rumus C Ke F Konversi Suhu
• Mengetahui Rumus Current Ratio