Halo pengunjung artikel rumusrumus.com sudahkah kamu siap untuk melanjutkan pembahasan yang pada artikel sebelumnya telah membahas atau mengupas materi tentang pertidaksamaan rasional, Nah pada artikel kali ini akan membahas mengenai materi, jenis2, dan contoh pertidaksamaan irasional beserta dengan bagaimana cara menyelesaikannya ?

Nah buat kalian yang membutuhkannya jangan khawatir semua yang kamu butuhkan ada disini. Agar kamu tidak bingung, marilah disimak pembahasan materi pertidaksamaan irasional secara rinci dibawah ini.
Pengertian Pertidaksamaan Irasional
Pertidaksamaan Irasional merupakan suatu bentuk pertidaksamaan yang memuat variabel di dalam tanda akarnya. Bentuk umum pertidaksamaan irasional ialah sebagai berikut ini :

Misal

Langkah – Langkah Penyelesaian
Setelah membaca penjelasan diatas, dibawah ini ada teknik langkah agar dapat menyelesaikan soal pertidaksamaan irasional :
- Pertama menguadratkan kedua ruas pertidaksamaannya supaya bentuk akarnya menjadi hilang, setelah itu menentukan penyelesaiannya.
- Kedua menetapkan syarat bagi fungsi yang berada tepat di bawah tanda akar. Tiap fungsi yang berada di bawah tanda akar tersebut harus menghasilkan nilai yang positif ataupun sama dengan nol (≥ 0).
- Dan yang terakhir menentukan irisan antara penyelesaian utama dengan syarat-syaratnya sehingga dapat diperoleh penyelesaian dari pertidaksamaan irasional tersebut.
Jenis – Jenis Pertidaksamaan Irasional
Berdasarkan langkah – langkah pertidaksamaan irasional diatas, dapat diperoleh bentuk kesimpulan sebagai berikut ini :
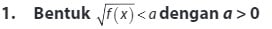
Bentuk ini dapat terpenuhi jika :
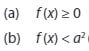
“Tergantung pada tanda pertidaksamaan yang diberikan”.
Penyelesaian : Merupakan irisan dari (a) dan (b)
Contoh :
Tentukanlah himpunan penyelesaian atas pertidaksamaan dibawah ini :
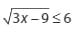
Jawaban :
Bentuk tersebut dapat terpenuhi jika diperoleh :
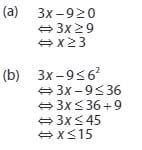
Penyelesaian himpunan pertidaksamaan irasional ini merupakan suatu irisan dari (a) dan (b). Sehingga diperoleh hasil :

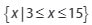
Berdasarkan penjelasan diatas dapat disimpulkan jika hasil himpunan penyelesaian atas pertidaksamaan tersebut ialah disamping ini
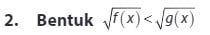
Bentuk ini dapat terpenuhi jika :
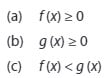
” Sesuai tanda ketidaksamaan yang diberikan”.
Penyelesaian : Merupakan irisan dari (a), (b), dan (c)
Contoh :
Tentukanlah himpunan penyelesaian atas pertidaksamaan dibawah ini :
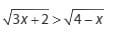
Jawaban :
Bentuk tersebut dapat dipenuhi jika :

Penyelesaian pertidaksamaan irasional adalah suatu irisan dari (a), (b), dan (c). Sehingga diperoleh hasil :
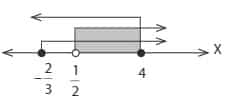
Berdasarkan hasil yang diperoleh diatas dapat disimpulkan hasil dari pertidaksamaan tersebut dibawah ini
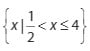
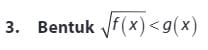
Bentuk ini dapat terpenuhi jika :

Penyelesaian : Merupakan irisan dari (a), (b), dan (c).
Contoh :
Tentukanlah himpunan penyelesaian dari pertidaksamaan dibawah ini
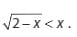
Jawaban :
Bentuk tersebut dapat dipenuhi jika

Titik pembuat nol adalah x = -2, x =1.
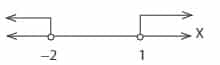
Penyelesaian : x < -2 dan x > 1
Penyelesaian pertidaksamaan irsional merupakan irisan dari (a), (b), dan (c). Sehingga diperoleh :
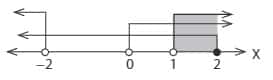
Hasil penyelesaian himpunan pertidaksamaan adalah dibawah ini
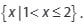
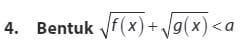
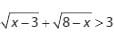
Himpunan penyelesaian dari pertidaksamaan
adalah
A. x > 7
B. 4 < x < 7
C. x < 4
D. -4 < x < 7
E.
Jawaban :
Bentuk tersebut dapat terpenuhi jika :

Titik pembuat nol x = 4, dan x = 7 adalah sebagai berikut :

Penyelesaian : 4 < x < 7
Penyelesaian himpunan pertidaksamaan irasional merupakan irisan dari (a), (b), dan (c). Sehingga dapat diperoleh sebagai berikut

Jadi dapat disimpulkan himpunan dari penyelesaian pertidaksamaan diatas adalah 4 < x < 7.
Pertidaksamaan Irasional adalah suatu bentuk pertidaksamaan dimana memuat variabel-variabel yang berada di dalam tanda akarnya.
1. Langkah awal yaitu menguadratkan kedua ruas pertidaksamaannya agar bentuk akarnya dapat hilang, lalu menentukan penyelesaiannya.
2. Langkah berikutnya adalah menetapkan syarat bagi fungsi yang berada tepat di bawah tanda akar. Tiap fungsi yang berada di bawah tanda akar ituharus menghasilkan nilai yang positif ataupun sama dengan nol (≥ 0) hasilnya.
3. Langkah terakhir menentukan irisan antara penyelesaian utama dengan syarat-syaratnya sehingga dapat diperoleh penyelesaian dari pertidaksamaan irasional tersebut.
Bilangan tidak bulat, dan angka berada dalam pangkat
Demikianlah pembahasan artikel kali ini, semoga bermanfaat dan menjadi ilmu pengetahuan baru bagi para pembaca.
Baca juga artikel lainnya :