Dalam rumus matematika terdapat rumus d fungsi kuadrat yang memang sudah tak asing lagi didengar. Fungsi kuadrat merupakan suatu persamaan dari variabel yang memiliki pangkat tertinggi dua. Fungsi ini berhubungan dengan persamaan kuadrat. Untuk lebih jelasnya, anda simak saja ulasan lengkapnya di bawah ini.
Rumus D Fungsi Kuadrat
Bentuk umum persamaan kuadrat atau rumus d fungsi kuadrat ialah sebagai berikut.
Sementara bentuk umum fungsi kuadrat yaitu:
Dengan a, b, adalah koefisien, c merupakan konstanta, dan .
Fungsi kuadrat f(x) juga bisa ditulis dalam bentuk y seperti berikut.
Dengan x merupakan variable bebas dan y ialah variable terikat. Dengan begitu, nilai y tergantung dari nilai x, dan nilai-nilai x dipengaruhi oleh area yang ditetapkan. Nilai y didapat dengan memasukan nilai-nilai x ke dalam fungsi.
Contoh Soal dan Penyelesaian
Supaya anda bisa lebih memahami rumus fungsi kuadrat, berikut kami bagikan contoh soal lengkap dengan penyelesaiannya berikut ini.
Contoh 1
Kerjakan x2 – 4 x + 3 = 0
Penyelesaian
Diketahui x2 – 4 x + 3 = 0
(x – 3) (x – 1) = 0
maka x – 3 = 0 atau x – 1 = 0
x = 3 atau x = 1
Dengan begitu, penyelesaian dari x2 – 4 x + 3 = 0 ialah 3 dan 1.
Contoh 2
Tentukan penyelesaian dari 2 x2 + 7 x + 6 = 0.
Penyelesaian
2 x2 + 7 x + 6 = 0
berarti 2 x2 + 4 x + 3 x + 6 = 0
maka 2 x (x + 2) + 3 (x + 2) = 0
hasilnya (x + 2) (2 x + 3) = 0
x +2 = 0 atau 2 x + 3 = 0
maka x = – 1 atau bisa juga x = –2
Penyelesaiannya ialah –2 dan –1.
Contoh 3
Selesaikan soal (x – 2)2 = x – 2!
Penyelesaian
Diketahui (x – 2)2 = x – 2
x2 – 4 x + 4 = x – 2
x2 – 5 x + 6 = 0
maka 0 = (x – 3) (x – 2)
x – 3 = 0 atau bisa juga x – 2 = 0
Jadi, x = 3 atau x = 2
Himpunan penyelesaiannya ialah {3 , 2}.
Contoh 4
Himpunan penyelesaian x2 – 6 x + 5 = 0?.
Penyelesaian
Diketahui x2 – 6 x + 5 = 0
berarti x2 – 6 x + 9 – 4 = 0
x2 – 6 x + 9 = 4
maka (x – 3)2 = 4
jadi x – 3 = 2 atau x – 3 = –2
x = 5 atau x = 1
Dengan begitu, himpunan penyelesaiannya {1 , 5}.
Contoh 5
Tentukan penyelesaian dari 2 x2 – 8 x + 7 = 0.
Penyelesaian
Diketahui 2 x2 – 8 x + 7 = 0
2 x2 – 8 x + 8 – 1 = 0
2 x2 – 8 x + 8 = 1
maka 2 (x2 – 4 x + 4) = 1
2 (x – 2)2 = 1
(x – 2)2 = ½
x – 2 = – atau bisa juga x – 2 =
x = 2 + Ö2 atau x = 2 –Ö2
Penyelesaiannya ialah 2 + Ö2 dan 2 – Ö2.
Contoh 6
Himpunan penyelesaian x2 + 7x – 30 = 0?.
Penyelesaian
x2 + 7x – 30 = 0
Diketahui a = 1 , b = 7 , c = – 30
x = 3 atau x = –10
Jadi, himpunan penyelesaiannya adalah {–10 , 3}.
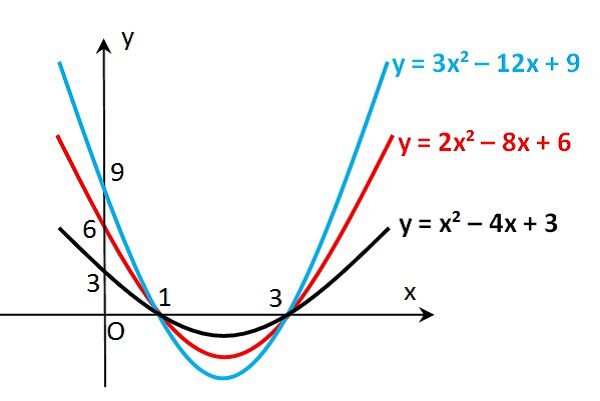
Grafik Fungsi Kuadrat
Fungsi kuadrat bisa digambarkan ke dalam koordinat kartesius. Dengan begitu, didapat suatu grafik fungsi kuadrat. Sumbu x merupakan domain serta sumbu y ialah kodomain. Grafik dari fungsi kuadrat dibentuk seperti parabola. Dengan begitu, sering disebut dengan grafik parabola. Grafik bisa dibuat dengan memasukan nilai x dalam interval tertentu. Jadi, nantinya akan didapat nilai y. Lalu pasangan nilai (x, y) ini menjadi koordinat dari yang dilalui suatu grafik. Mengenai jenisnya, grafik fungsi kuadrat terdapat beberapa jenis. Berikut ulasannya.
Grafik fungsi 
Apabila pada fungsi mempunyai nilai b dan c sama dengan nol, maka fungsi kuadrat ialah sebagai berikut.
Grafik fungsi 
Apabila pada fungsi mempunyai nilai b = 0, maka fungsi kuadratnya yaitu:
Dalam fungsi ini, grafik bisa mempunyai kesamaan dengan grafik fungsi kuadrat , yakni selalu mempunyai garis simetris pada x = 0. Akan tetapi, titik puncak sama dengan nilai c atau
.
Grafik fungsi 
Grafik ini adalah hasil perubahan bentuk dari . Dalam fungsi kuadrat yang satu ini, grafik akan mempunyai titik puncak (x, y) sama dengan (h, k). Keterkaitan antara a, b, serta c dengan h dan k ialah sebagai berikut.
Sama halnya rumus matematika lainnya, rumus d fungsi kuadrat ini penting untuk diketahui dan dipelajari.