Rumusrumus.com – kali ini akan membahas tentang tabel kebenaran logika matematika meliputi dari pengertian dari masing – masing tabel kebenaran yaitu tabel kebenaran konjungsi, Disjungsi, Implikasi, ingkaran (negasi), biimplikasi, negasi konjungsi, negasi disjungsi, negasi implikasi, dan negasi biimplikasi.
Pengertian Tabel Kebenaran
Pada logika matematika, tabel kebenaran adalah tabel didalam matematika yang dipakai untuk melihat nilai kebenaran pada suatu premis ataupun pernyataan. Jika hasil akhir ialah benar semua (dilambangkan dengan B, T, atau 1), maka disebut tautologi. Akan tetapi jika salah semua (S, F, atau 0) disebut kontradiksi. Premis hasil akhirnya gabungan benar dan salah disebut kontingensi.
Tabel Kebenaran Ingkaran (Negasi)
| p | ~p |
| B | S |
| S | B |
Keterangan :
Maksud B dan S pada tabel ialah B itu Bernilai benar dan S bernilai salah.
Tabel Kebenaran Konjungsi
Konjungsi ialah gabungan dari dua pernyataan tunggal dengan memakai kata hubung “dan“. Simbol dari konjungsi alah “^“. Untuk Lebih jelas perhatikan gambar di bawah ini :
| p | q | p^q |
| B | B | B |
| B | S | S |
| S | B | S |
| S | S | S |
Tabel kebenaran itu pun ada hukumnya, jika nilai kedua pernyataan benar, maka nilai kebenaran konjungsi kedua pernyataan itu pun benar, namun apabila ada salah satu pernyataan yang salah, maka nilai konjungsi kedua pernyataan tersebut pun memiliki nilai salah.
Tabel Kebenaran Disjungsi
Disjungsi ialah gabungan dari dua pernyataan tunggal dan yang menggunakan kata hubung “atau“. Simbol dari disjungsi ialah “CodeCogsEqn (1) “. Untuk tabel kebenaran disjjungsi perhatikan gambar di bawah ini :
| p | q | pvq |
| B | B | B |
| B | S | B |
| S | B | B |
| S | S | S |
Dalam menentukan nilai kebenaran disjungsi juga mempunyai aturan yaitu, andai salah satu dari dua pernyataan memiliki nilai benar, maka nilai kebenaran disjungsi dari kedua pernyataan itu adalah benar, namun apabila kedua pernyataan tersebut memiliki nilai salah, maka nilai kebenaran disjungsi pun bernilai salah.
Tabel Kebenaran Implikasi
Impilakasi ialah gabungan dari dua pernyataan tunggal dengan kata hubung “jika” dan “maka“. Simbol dari implikasi yaitu “→“. Tabel kebenarannya perhatikan pada gambar di bawah ini :
| p | q | p → q |
| B | B | B |
| B | S | S |
| S | B | B |
| S | S | B |
Pada aturan menentukan nilai kebenaran dari implikasi ialah, jika nilai pernyataan yang ke dua dari dua pernyataan memiliki nilai benar dan jika ke dua pernyataan bernilai sama baik itu benar ataupun salah, jadi nilai kebenaran implikasi yaitu benar, namun apabila nilai kedua pernyataan itu berbeda dengan pernyataan ke duanya bernilai salah, maka nilai kebenaran implikasi dari dua pernyatan tersebut memiliki nilai salah.
Tabel Kebenaran Biimplikasi
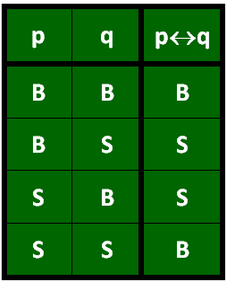
Biimplikasi ialah gabungan dari dua pernyataan tunggal dengan kata hubung “jika dan hanya jika, maka “. Simbol dari biimplikasi yaitu “↔“. Contoh tabel untuk nilai kebenaran biimplikasi perhatikan tebel di bawah ini :
Pada aturan nilai kebenaran biimplikasi yaitu, Andai Kedua pernyataan sama, maka nilai kebenaran biimplikasi benar, begitupun sebaliknya andai nilai salah satu dari pernyataan bernilai salah maka nilai kebenaran dari biimplikasi dari kedua pernyataan tersebut adalah salah.
Tabel Kebenaran Negasi Konjungsi
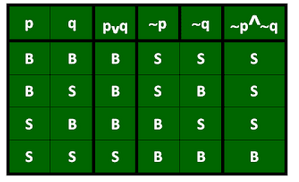
Pada tabel kebenaran negasi konjungsi ini berlaku negasi dari p ∧ q equivalen dengan ~p ∨ ~q. Contoh tabel kebenaran negasi konjungsi lihat tabel di bawah :
Tabel Kebenaran Negasi Disjungsi
Pada nilai kebenaran disjungsi berlaku negasi dari p ∨ q ekuivale dengan ~p ∧ ~q. Contoh tabel kebenaran negasi disjungsi perhatikan tabel di bawah :
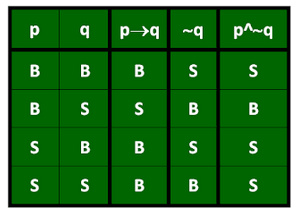
Tabel Kebenaran Negasi Implikasi
Pada nilai kebenaran negasi implikasi ialah negasi dari p→q ekuivalen dengan p∧~q , contoh tabel kebenaran nrgasi implikasi seperti contoh dibawah ini
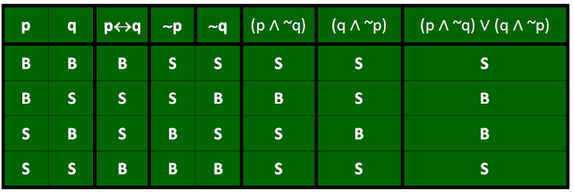
Tabel Kebenaran Negasi Biimplikasi
Negasi dari p↔q ekuivalen dengan (p ∧ ~q) ∨ (q ∧ ~p)
Contoh nilai kebenaran negasi biimplikasi seperti dibawah ini
Maka untuk menentukan pernyataan bernilai benar ataupun salah, dalam ilmu logika matematika yaitu dengan cara menentukan tabel kebenaran. semoga bermanfaat…
Artikel lainya: