Rumusrumus.com kali ini akan membahas tentang pengertian dan persamaan garis singgung lingkaran beserta contoh soalnya dan menjelaskan tentang berbagai metode cara penyelesaianya
Pengertian Garis Singgung Lingkaran
Garis singgung lingkaran yaitu garis yang menyinggung pada suatu lingkaran. Bila suatu garis menyinggung lingkaran, maka garis itu tepat melalui satu titik pada (pinggir) lingkaran.
Persamaan Garis Singgung Lingkaran
Persamaan garis singgung pada suatu lingkaran bisa ditentukan dengan berbagai cara, bergantung pada informasi-informasi apa yang di ketahui dari garis singgung tersebut.
Persamaan Garis Singgung Lingkaran Melalui Suatu Titik
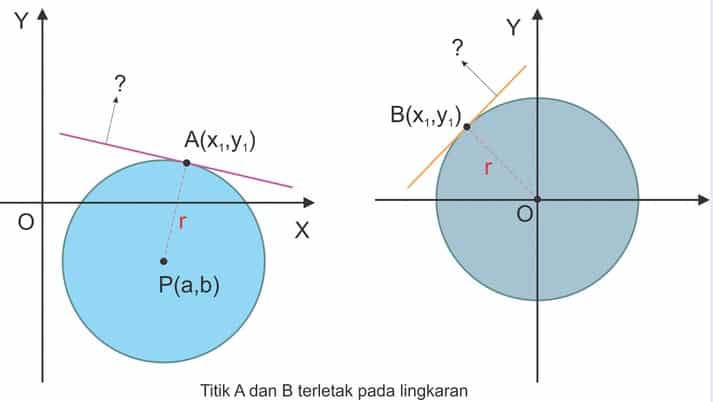
Untuk hal ini akan dibagi menjadi 2, yaitu persamaan garis singgung lingkaran melalui titik pada lingkaran dan persamaan garis singgung lingkaran yang melalui titik di luar lingkaran.
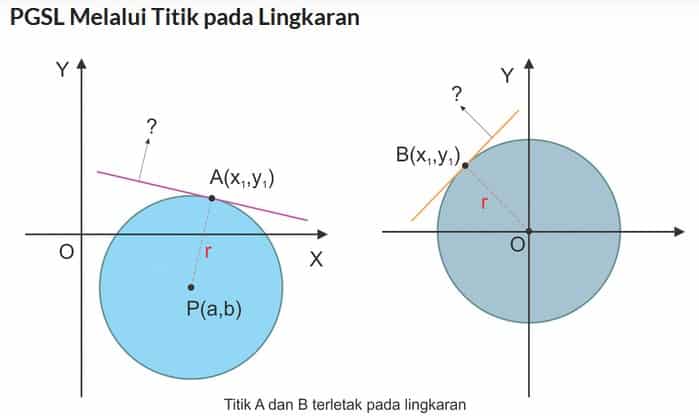
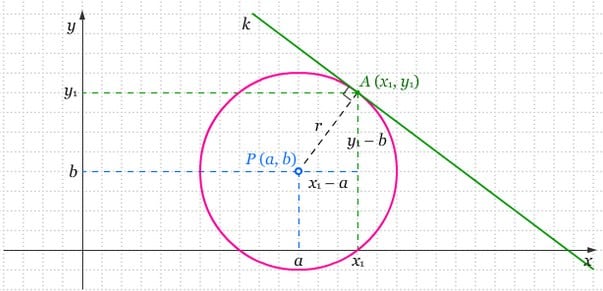
Persamaan garis singgung lingkaran (x−a)2+(y−b)2=r2 melalui titik (x1, y1) yaitu (x1−a)(x−a)+(y1−b)(y−b)=r2 dengan
(a, b) yaitu pusat lingkaran
r yaitu radius ataupun jari-jari lingkaran
(x1, y1) yaitu titik singgung lingkaran
Persamaan garis singgung lingkaran x2 + y2 = r2 melalui titik (x1, y1) ialah x1x+y1y=r2 dengan
r adalah radius atau jari-jari lingkaran
(x1, y1) adalah titik singgung lingkaran
Persamaan Garis Singgung Melalui Titik di Luar Lingkaran
Ada dua garis singgung yang bisa dibuat dari titik yang berada diluar lingkaran. Untuk menentukan kedua persamaan garis singgung itu, terlebih dahulu tentukan titik singgung hingga garis singgung di titik itu melalui titik yang berada diluar lingkaran.
Ada berbagai cara untuk menentukan titik-titik singgung tersebut, salah satunya yaitu dengan menggunakan bantuan garis polar ataupun kutub. Persamaan garis polar bisa ditentukan dengan menggunakan rumus persamaan garis singgung yang sebelumnya dimana (x1, y1) yaitu titik yang berada diluar lingkaran.
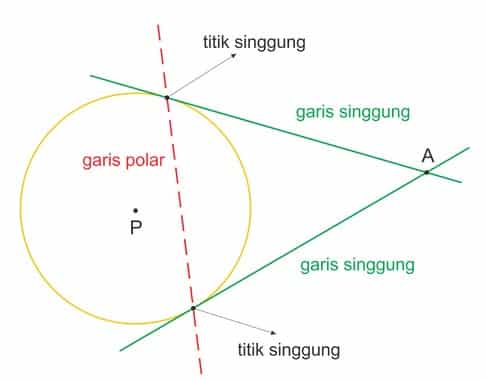
Karena garis polar memotong lingkaran tepat pada titik singgung, maka titik-titik singgung itu bisa ditentukan dengan mensubstitusi persamaan garis polar ke persamaan lingkaran
Contoh Soal
Contoh Soal 1
Persamaan garis singgung lingkaran melalui titik A (x1, y1) pada lingkaran yang berpusat pada titik (a, b) dan berjari-jari r.
Tentukan rumus dan persamaan gatis singgung dari ilustrasi gambar tersebut :
Jawab
L = (x – a)2 + (y – b)2 = r2
persamaan garis singgungnya ialah :
(x – a)(x1 – a) + (y – b)(y1 – b) = r2.
Contoh Soal 2
Tentukanlah persamaan garis singgung Lingkaran
L = (x – 1)2 + (y – 4)2 = 25 dan Titik singgung A (-3 , 1) .
Jawab
Diketahui :
x1 = -3, y1 = 1
L = (x – 1)2 + (y – 4)2 = 25
a = 1 , b = 4 dan r2 = 25
Jadi (masukan ke persamaan)
(x -1) (-3 – 1) + (y – 4) (1 – 4) = 25
(x-1) (- 4) + (y – 4) (-3) = 25
-4x + 4 – 3y + 12 = 25
-4x – 3y + 16 = 25
-4x – 3y + 16 – 25 = 0
-4x – 3y – 9 = 0 atau 4x + 3y = 9 = 0
Contoh Soal 3 :
Tentukan persamaan garis singgung melalui titik (2, –3) pada lingkaran
x2 + y2 = 13.
Jawab
Diketahui : x1 = 2, y1 = –3 dan L = x2 + y2 = 13
Jadi :
x1 x + y1 y = r2
2x + (-3) y = 13
2x – 3y = 13
2x – 3y – 13 = 0
Contoh Soal 4
Tentukan persamaan garis singgung lingkaran x2 + y2 = 25 melalui titik (3, 4)
Jawab :
diketahui
P (0, 0)
r2 = 25
(x1, y1) = (3, 4)
Persamaan garis singgungnya
x1 x + y1 y = r2
⇔ 3x + 4y = 25
Demikianlah penjelasan tentang garis singgung suatu lingkaan baik dari titik dalam maupun daari titik luar lingkaran beserta contoh soal daai Rumusrumus.com, Semoga bermanfaat
Artikel Lainya :